Functions | |
| RBDL_DLLAPI void | InverseDynamics (Model &model, const Math::VectorNd &Q, const Math::VectorNd &QDot, const Math::VectorNd &QDDot, Math::VectorNd &Tau, std::vector< Math::SpatialVector > *f_ext=NULL) |
| Computes inverse dynamics with the Newton-Euler Algorithm. More... | |
| RBDL_DLLAPI void | NonlinearEffects (Model &model, const Math::VectorNd &Q, const Math::VectorNd &QDot, Math::VectorNd &Tau, std::vector< Math::SpatialVector > *f_ext=NULL) |
| Computes the coriolis forces. More... | |
| RBDL_DLLAPI void | CompositeRigidBodyAlgorithm (Model &model, const Math::VectorNd &Q, Math::MatrixNd &H, bool update_kinematics=true) |
| Computes the joint space inertia matrix by using the Composite Rigid Body Algorithm. More... | |
| RBDL_DLLAPI void | ForwardDynamics (Model &model, const Math::VectorNd &Q, const Math::VectorNd &QDot, const Math::VectorNd &Tau, Math::VectorNd &QDDot, std::vector< Math::SpatialVector > *f_ext=NULL) |
| Computes forward dynamics with the Articulated Body Algorithm. More... | |
| RBDL_DLLAPI void | ForwardDynamicsLagrangian (Model &model, const Math::VectorNd &Q, const Math::VectorNd &QDot, const Math::VectorNd &Tau, Math::VectorNd &QDDot, Math::LinearSolver linear_solver=Math::LinearSolverColPivHouseholderQR, std::vector< Math::SpatialVector > *f_ext=NULL, Math::MatrixNd *H=NULL, Math::VectorNd *C=NULL) |
| Computes forward dynamics by building and solving the full Lagrangian equation. More... | |
| RBDL_DLLAPI void | CalcMInvTimesTau (Model &model, const Math::VectorNd &Q, const Math::VectorNd &Tau, Math::VectorNd &QDDot, bool update_kinematics=true) |
| Computes the effect of multiplying the inverse of the joint space inertia matrix with a vector in linear time. More... | |
Detailed Description
Function Documentation
◆ CalcMInvTimesTau()
| RBDL_DLLAPI void RigidBodyDynamics::CalcMInvTimesTau | ( | Model & | model, |
| const Math::VectorNd & | Q, | ||
| const Math::VectorNd & | Tau, | ||
| Math::VectorNd & | QDDot, | ||
| bool | update_kinematics = true |
||
| ) |
Computes the effect of multiplying the inverse of the joint space inertia matrix with a vector in linear time.
- Parameters
-
model rigid body model Q state vector of the generalized positions Tau the vector that should be multiplied with the inverse of the joint space inertia matrix QDDot vector where the result will be stored update_kinematics whether the kinematics should be updated (safer, but at a higher computational cost)
This function uses a reduced version of the Articulated Body Algorithm to compute:
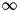
for given 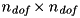 and
and 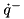 in
in 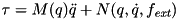 time.
time.
- Note
- When calling this function repeatedly for the same values of Q make sure to set the last parameter to false as this avoids expensive recomputations of transformations and articulated body inertias.
◆ CompositeRigidBodyAlgorithm()
| RBDL_DLLAPI void RigidBodyDynamics::CompositeRigidBodyAlgorithm | ( | Model & | model, |
| const Math::VectorNd & | Q, | ||
| Math::MatrixNd & | H, | ||
| bool | update_kinematics = true |
||
| ) |
Computes the joint space inertia matrix by using the Composite Rigid Body Algorithm.
This function computes the joint space inertia matrix from a given model and the generalized state vector: 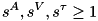
- Parameters
-
model rigid body model Q state vector of the model H a matrix where the result will be stored in update_kinematics whether the kinematics should be updated (safer, but at a higher computational cost!)
- Note
- This function only evaluates the entries of H that are non-zero. One Before calling this function one has to ensure that all other values have been set to zero, e.g. by calling H.setZero().
◆ ForwardDynamics()
| RBDL_DLLAPI void RigidBodyDynamics::ForwardDynamics | ( | Model & | model, |
| const Math::VectorNd & | Q, | ||
| const Math::VectorNd & | QDot, | ||
| const Math::VectorNd & | Tau, | ||
| Math::VectorNd & | QDDot, | ||
| std::vector< Math::SpatialVector > * | f_ext = NULL |
||
| ) |
Computes forward dynamics with the Articulated Body Algorithm.
This function computes the generalized accelerations from given generalized states, velocities and forces: 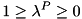 It does this by using the recursive Articulated Body Algorithm that runs in
It does this by using the recursive Articulated Body Algorithm that runs in 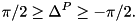 with
with 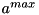 being the number of joints.
being the number of joints.
- Parameters
-
model rigid body model Q state vector of the internal joints QDot velocity vector of the internal joints Tau actuations of the internal joints QDDot accelerations of the internal joints (output) f_ext External forces acting on the body in base coordinates (optional, defaults to NULL)
◆ ForwardDynamicsLagrangian()
| RBDL_DLLAPI void RigidBodyDynamics::ForwardDynamicsLagrangian | ( | Model & | model, |
| const Math::VectorNd & | Q, | ||
| const Math::VectorNd & | QDot, | ||
| const Math::VectorNd & | Tau, | ||
| Math::VectorNd & | QDDot, | ||
| Math::LinearSolver | linear_solver = Math::LinearSolverColPivHouseholderQR, |
||
| std::vector< Math::SpatialVector > * | f_ext = NULL, |
||
| Math::MatrixNd * | H = NULL, |
||
| Math::VectorNd * | C = NULL |
||
| ) |
Computes forward dynamics by building and solving the full Lagrangian equation.
This method builds and solves the linear system
![\[ H \ddot{q} = -C + \tau \]](../../form_154.png)
for 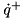 where
where 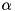 is the joint space inertia matrix computed with the CompositeRigidBodyAlgorithm(),
is the joint space inertia matrix computed with the CompositeRigidBodyAlgorithm(), 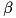 the bias force (sometimes called "non-linear effects").
the bias force (sometimes called "non-linear effects").
- Parameters
-
model rigid body model Q state vector of the internal joints QDot velocity vector of the internal joints Tau actuations of the internal joints QDDot accelerations of the internal joints (output) linear_solver specification which method should be used for solving the linear system f_ext External forces acting on the body in base coordinates (optional, defaults to NULL) H preallocated workspace area for the joint space inertia matrix of size dof_count x dof_count (optional, defaults to NULL and allocates temporary matrix) C preallocated workspace area for the right hand side vector of size dof_count x 1 (optional, defaults to NULL and allocates temporary vector)
◆ InverseDynamics()
| RBDL_DLLAPI void RigidBodyDynamics::InverseDynamics | ( | Model & | model, |
| const Math::VectorNd & | Q, | ||
| const Math::VectorNd & | QDot, | ||
| const Math::VectorNd & | QDDot, | ||
| Math::VectorNd & | Tau, | ||
| std::vector< Math::SpatialVector > * | f_ext = NULL |
||
| ) |
Computes inverse dynamics with the Newton-Euler Algorithm.
This function computes the generalized forces from given generalized states, velocities, and accelerations: 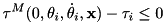
- Parameters
-
model rigid body model Q state vector of the internal joints QDot velocity vector of the internal joints QDDot accelerations of the internals joints Tau actuations of the internal joints (output) f_ext External forces acting on the body in base coordinates (optional, defaults to NULL)
◆ NonlinearEffects()
| RBDL_DLLAPI void RigidBodyDynamics::NonlinearEffects | ( | Model & | model, |
| const Math::VectorNd & | Q, | ||
| const Math::VectorNd & | QDot, | ||
| Math::VectorNd & | Tau, | ||
| std::vector< Math::SpatialVector > * | f_ext = NULL |
||
| ) |
Computes the coriolis forces.
This function computes the generalized forces from given generalized states, velocities, and accelerations: 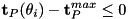
- Parameters
-
model rigid body model Q state vector of the internal joints QDot velocity vector of the internal joints Tau actuations of the internal joints (output) f_ext External forces acting on the body in base coordinates (optional, defaults to NULL)