Data Structures | |
| struct | ConstraintSet |
| Structure that contains both constraint information and workspace memory. More... | |
Functions | |
| ConstraintSet () | |
| unsigned int | getGroupIndexByName (const char *userDefinedName) |
| getGroupIndex returns the index to a constraints that have been grouped because they are of the same type, apply to the same bodies, and apply to the same local frames on each body. More... | |
| unsigned int | getGroupIndexById (unsigned int userDefinedId) |
| getGroupIndex returns the index to a constraints that have been grouped because they are of the same type, apply to the same bodies, and apply to the same local frames on each body. More... | |
| unsigned int | getGroupIndexByAssignedId (unsigned int assignedId) |
| getGroupIndex returns the index to a constraints that have been grouped because they are of the same type, apply to the same bodies, and apply to the same local frames on each body. More... | |
| unsigned int | getGroupIndexMax () |
| getGroupIndexMax returns the maximum valid constraint group index (the min. is zero) so that constraint groups can be iterated over if desired. More... | |
| const char * | getGroupName (unsigned int groupIndex) |
| Returns the name of the constraint group, which may differ from the names entered by the user if the constraint is one in which grouping is done automatically (e.g. contact and loop constraints) More... | |
| unsigned int | getGroupSize (unsigned int groupIndex) |
| Returns the number of constraint equations in this group. More... | |
| unsigned int | getGroupType (unsigned int groupIndex) |
| Returns integer corresponding to the ConstraintType. More... | |
| unsigned int | getGroupId (unsigned int groupIndex) |
| Returns the user-defined-id of the constraint group, which may differ from the names entered by the user if the constraint is one in which grouping is done automatically (e.g. contact and loop constraints). More... | |
| unsigned int | getGroupAssignedId (unsigned int groupIndex) |
| Returns assigned id of the constraint group which will be the first id assigned to an entry in a group (if the grouping was done automatically - as is done for contact and loop constraints). More... | |
| void | calcForces (unsigned int groupIndex, Model &model, const Math::VectorNd &Q, const Math::VectorNd &QDot, std::vector< unsigned int > &updConstraintBodyIdsOutput, std::vector< Math::SpatialTransform > &updConstraintBodyFramesOutput, std::vector< Math::SpatialVector > &updConstraintForcesOutput, bool resolveAllInRootFrame=false, bool updateKinematics=false) |
| calcForces resolves the generalized forces generated by this constraint into equivalent spatial forces (resolved in the local or the base frame) that are applied between the bodies and frames that this constraint applies to. More... | |
| void | calcImpulses (unsigned int groupIndex, Model &model, const Math::VectorNd &Q, const Math::VectorNd &QDot, std::vector< unsigned int > &constraintBodyIdsOutput, std::vector< Math::SpatialTransform > &constraintBodyFramesOutput, std::vector< Math::SpatialVector > &constraintImpulsesOutput, bool resolveAllInRootFrame=false, bool updateKinematics=false) |
| calcImpulses resolves the generalized impluses generated by this constraint into equivalent spatial impulses (resolved in the local or the base frame) that are applied between the bodies and frames that this constraint applies to. More... | |
| void | calcPositionError (unsigned int groupIndex, Model &model, const Math::VectorNd &Q, Math::VectorNd &positionErrorOutput, bool updateKinematics=false) |
| calcPositionError calculates the vector of position errors associated with this constraint. Note that if the constraint group, or parts of it, are not defined at the position level then 0's will be returned. More... | |
| void | calcVelocityError (unsigned int groupIndex, Model &model, const Math::VectorNd &Q, const Math::VectorNd &QDot, Math::VectorNd &velocityErrorOutput, bool updateKinematics=false) |
| calcVelocityError calculates the vector of position errors associated with this constraint. Note that if the constraint group, or parts of it, are not defined at the position level then 0's will be returned. More... | |
| void | calcBaumgarteStabilizationForces (unsigned int groupIndex, Model &model, const Math::VectorNd &positionError, const Math::VectorNd &velocityError, Math::VectorNd &baumgarteForcesOutput) |
| bool | isBaumgarteStabilizationEnabled (unsigned int groupIndex) |
| void | enableBaumgarteStabilization (unsigned int groupIndex) |
| void | disableBaumgarteStabilization (unsigned int groupIndex) |
| void | getBaumgarteStabilizationCoefficients (unsigned int groupIndex, Math::Vector2d &baumgartePositionVelocityCoefficientsOutput) |
| unsigned int | AddContactConstraint (unsigned int bodyId, const Math::Vector3d &bodyPoint, const Math::Vector3d &worldNormal, const char *constraintName=NULL, unsigned int userDefinedId=std::numeric_limits< unsigned int >::max()) |
| Adds a single contact constraint (point-ground) to the constraint set. More... | |
| unsigned int | AddLoopConstraint (unsigned int bodyIdPredecessor, unsigned int bodyIdSuccessor, const Math::SpatialTransform &XPredecessor, const Math::SpatialTransform &XSuccessor, const Math::SpatialVector &constraintAxisInPredecessor, bool enableBaumgarteStabilization=false, double stabilizationTimeConstant=0.1, const char *constraintName=NULL, unsigned int userDefinedId=std::numeric_limits< unsigned int >::max()) |
| Adds a loop constraint to the constraint set. More... | |
| unsigned int | AddCustomConstraint (std::shared_ptr< Constraint > customConstraint) |
| Adds a custom constraint to the constraint set. More... | |
| ConstraintSet | Copy () |
| Copies the constraints and resets its ConstraintSet::bound flag. More... | |
| void | SetSolver (Math::LinearSolver solver) |
| Specifies which method should be used for solving undelying linear systems. More... | |
| bool | Bind (const Model &model) |
| Initializes and allocates memory for the constraint set. More... | |
| void | SetActuationMap (const Model &model, const std::vector< bool > &actuatedDof) |
| Initializes and allocates memory needed for InverseDynamicsConstraints and InverseDynamicsConstraintsRelaxed. More... | |
| size_t | size () const |
| Returns the number of constraints. More... | |
| void | clear () |
| Clears all variables in the constraint set. More... | |
| RBDL_DLLAPI void | CalcConstraintsPositionError (Model &model, const Math::VectorNd &Q, ConstraintSet &CS, Math::VectorNd &errOutput, bool update_kinematics=true) |
| Computes the position errors for the given ConstraintSet. More... | |
| RBDL_DLLAPI void | CalcConstraintsJacobian (Model &model, const Math::VectorNd &Q, ConstraintSet &CS, Math::MatrixNd &GOutput, bool update_kinematics=true) |
| Computes the Jacobian for the given ConstraintSet. More... | |
| RBDL_DLLAPI void | CalcConstraintsVelocityError (Model &model, const Math::VectorNd &Q, const Math::VectorNd &QDot, ConstraintSet &CS, Math::VectorNd &errOutput, bool update_kinematics=true) |
| Computes the velocity errors for the given ConstraintSet. More... | |
| RBDL_DLLAPI void | CalcConstrainedSystemVariables (Model &model, const Math::VectorNd &Q, const Math::VectorNd &QDot, const Math::VectorNd &Tau, ConstraintSet &CSOutput, bool update_kinematics=true, std::vector< Math::SpatialVector > *f_ext=NULL) |
Computes the terms 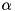 , , 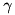 , and , and 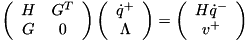 of the constrained dynamic problem and stores them in the ConstraintSet. More... of the constrained dynamic problem and stores them in the ConstraintSet. More... | |
| RBDL_DLLAPI bool | CalcAssemblyQ (Model &model, Math::VectorNd QInit, ConstraintSet &CS, Math::VectorNd &QOutput, const Math::VectorNd &weights, double tolerance=1e-12, unsigned int max_iter=100) |
| Computes a feasible initial value of the generalized joint positions. More... | |
| RBDL_DLLAPI void | CalcAssemblyQDot (Model &model, const Math::VectorNd &Q, const Math::VectorNd &QDotInit, ConstraintSet &CS, Math::VectorNd &QDotOutput, const Math::VectorNd &weights) |
| Computes a feasible initial value of the generalized joint velocities. More... | |
| RBDL_DLLAPI void | ForwardDynamicsConstraintsDirect (Model &model, const Math::VectorNd &Q, const Math::VectorNd &QDot, const Math::VectorNd &Tau, ConstraintSet &CS, Math::VectorNd &QDDotOutput, bool update_kinematics=true, std::vector< Math::SpatialVector > *f_ext=NULL) |
| Computes forward dynamics with contact by constructing and solving the full lagrangian equation. More... | |
| RBDL_DLLAPI void | ForwardDynamicsConstraintsRangeSpaceSparse (Model &model, const Math::VectorNd &Q, const Math::VectorNd &QDot, const Math::VectorNd &Tau, ConstraintSet &CS, Math::VectorNd &QDDotOutput, bool update_kinematics=true, std::vector< Math::SpatialVector > *f_ext=NULL) |
| RBDL_DLLAPI void | ForwardDynamicsConstraintsNullSpace (Model &model, const Math::VectorNd &Q, const Math::VectorNd &QDot, const Math::VectorNd &Tau, ConstraintSet &CS, Math::VectorNd &QDDotOutput, bool update_kinematics=true, std::vector< Math::SpatialVector > *f_ext=NULL) |
| RBDL_DLLAPI void | ForwardDynamicsContactsKokkevis (Model &model, const Math::VectorNd &Q, const Math::VectorNd &QDot, const Math::VectorNd &Tau, ConstraintSet &CS, Math::VectorNd &QDDotOutput) |
| Computes forward dynamics that accounts for active contacts in ConstraintSet. More... | |
| RBDL_DLLAPI void | InverseDynamicsConstraintsRelaxed (Model &model, const Math::VectorNd &Q, const Math::VectorNd &QDot, const Math::VectorNd &QDDotControls, ConstraintSet &CS, Math::VectorNd &QDDotOutput, Math::VectorNd &TauOutput, bool update_kinematics=true, std::vector< Math::SpatialVector > *f_ext=NULL) |
| A relaxed inverse-dynamics operator that can be applied to under-actuated or fully-actuated constrained multibody systems. More... | |
| RBDL_DLLAPI void | InverseDynamicsConstraints (Model &model, const Math::VectorNd &Q, const Math::VectorNd &QDot, const Math::VectorNd &QDDotDesired, ConstraintSet &CS, Math::VectorNd &QDDotOutput, Math::VectorNd &TauOutput, bool update_kinematics=true, std::vector< Math::SpatialVector > *f_ext=NULL) |
| An inverse-dynamics operator that can be applied to fully-actuated constrained systems. More... | |
| RBDL_DLLAPI bool | isConstrainedSystemFullyActuated (Model &model, const Math::VectorNd &Q, const Math::VectorNd &QDot, ConstraintSet &CS, bool update_kinematics=true, std::vector< Math::SpatialVector > *f_ext=NULL) |
| A method to evaluate if the constrained system is fully actuated. More... | |
| RBDL_DLLAPI void | ComputeConstraintImpulsesDirect (Model &model, const Math::VectorNd &Q, const Math::VectorNd &QDotMinus, ConstraintSet &CS, Math::VectorNd &QDotPlusOutput) |
| Computes contact gain by constructing and solving the full lagrangian equation. More... | |
| RBDL_DLLAPI void | ComputeConstraintImpulsesRangeSpaceSparse (Model &model, const Math::VectorNd &Q, const Math::VectorNd &QDotMinus, ConstraintSet &CS, Math::VectorNd &QDotPlusOutput) |
| Resolves contact gain using SolveContactSystemRangeSpaceSparse() More... | |
| RBDL_DLLAPI void | ComputeConstraintImpulsesNullSpace (Model &model, const Math::VectorNd &Q, const Math::VectorNd &QDotMinus, ConstraintSet &CS, Math::VectorNd &QDotPlusOutput) |
| Resolves contact gain using SolveContactSystemNullSpace() More... | |
| RBDL_DLLAPI void | SolveConstrainedSystemDirect (Math::MatrixNd &H, const Math::MatrixNd &G, const Math::VectorNd &c, const Math::VectorNd &gamma, Math::VectorNd &lambda, Math::MatrixNd &A, Math::VectorNd &b, Math::VectorNd &x, Math::LinearSolver &linear_solver) |
| Solves the full contact system directly, i.e. simultaneously for contact forces and joint accelerations. More... | |
| RBDL_DLLAPI void | SolveConstrainedSystemRangeSpaceSparse (Model &model, Math::MatrixNd &H, const Math::MatrixNd &G, const Math::VectorNd &c, const Math::VectorNd &gamma, Math::VectorNd &qddot, Math::VectorNd &lambda, Math::MatrixNd &K, Math::VectorNd &a, Math::LinearSolver linear_solver) |
| Solves the contact system by first solving for the the joint accelerations and then the contact forces using a sparse matrix decomposition of the joint space inertia matrix. More... | |
| RBDL_DLLAPI void | SolveConstrainedSystemNullSpace (Math::MatrixNd &H, const Math::MatrixNd &G, const Math::VectorNd &c, const Math::VectorNd &gamma, Math::VectorNd &qddot, Math::VectorNd &lambda, Math::MatrixNd &Y, Math::MatrixNd &Z, Math::VectorNd &qddot_y, Math::VectorNd &qddot_z, Math::LinearSolver &linear_solver) |
| Solves the contact system by first solving for the joint accelerations and then for the constraint forces. More... | |
Variables | |
| Math::LinearSolver | linear_solver |
| Method that should be used to solve internal linear systems. More... | |
| bool | bound |
| Whether the constraint set was bound to a model (mandatory!). More... | |
| std::vector< ConstraintType > | constraintType |
| std::vector< std::string > | name |
| std::map< std::string, unsigned int > | nameGroupMap |
| std::map< unsigned int, unsigned int > | userDefinedIdGroupMap |
| std::map< unsigned int, unsigned int > | idGroupMap |
| std::vector< std::shared_ptr< Constraint > > | constraints |
| std::vector< std::shared_ptr< ContactConstraint > > | contactConstraints |
| std::vector< std::shared_ptr< LoopConstraint > > | loopConstraints |
| Math::VectorNd | err |
| Math::VectorNd | errd |
| Math::VectorNd | force |
| Math::VectorNd | impulse |
| Constraint impulses along the constraint directions. More... | |
| Math::VectorNd | v_plus |
| The velocities we want to have along the constraint directions. More... | |
| Math::MatrixNd | H |
| Workspace for the joint space inertia matrix. More... | |
| Math::VectorNd | C |
| Workspace for the coriolis forces. More... | |
| Math::VectorNd | gamma |
| Workspace of the right hand side of the acceleration equation. More... | |
| Math::MatrixNd | G |
| Workspace for the constraint Jacobian. More... | |
| Math::MatrixNd | A |
| Workspace for the Lagrangian left-hand-side matrix. More... | |
| Math::VectorNd | b |
| Workspace for the Lagrangian right-hand-side. More... | |
| Math::VectorNd | x |
| Workspace for the Lagrangian solution. More... | |
| Math::MatrixNd | S |
| Math::MatrixNd | P |
| Selection matrix for the non-actuated parts of the model. More... | |
| Math::MatrixNd | W |
| Math::MatrixNd | Winv |
| Math::VectorNd | WinvSC |
| Math::VectorNd | u |
| Math::VectorNd | v |
| Math::MatrixNd | F |
| Math::MatrixNd | Ful |
| Math::MatrixNd | Fur |
| Math::MatrixNd | Fll |
| Math::MatrixNd | Flr |
| Math::MatrixNd | GT |
| Math::MatrixNd | GTu |
| Math::MatrixNd | GTl |
| Math::VectorNd | g |
| Math::MatrixNd | Ru |
| Math::VectorNd | py |
| Math::VectorNd | pz |
| Eigen::HouseholderQR< Math::MatrixNd > | GT_qr |
| Workspace for the QR decomposition of the null-space method. More... | |
| Eigen::FullPivHouseholderQR< Math::MatrixNd > | GPT_full_qr |
| Math::MatrixNd | GT_qr_Q |
| Math::MatrixNd | GPT |
| Math::MatrixNd | Y |
| Math::MatrixNd | Z |
| Math::MatrixNd | R |
| Math::VectorNd | qddot_y |
| Math::VectorNd | qddot_z |
| Math::MatrixNd | K |
| Workspace for the Inverse Articulated-Body Inertia. More... | |
| Math::VectorNd | a |
| Workspace for the accelerations of due to the test forces. More... | |
| Math::VectorNd | QDDot_t |
| Workspace for the test accelerations. More... | |
| Math::VectorNd | QDDot_0 |
| Workspace for the default accelerations. More... | |
| std::vector< Math::SpatialVector > | f_t |
| Workspace for the test forces. More... | |
| std::vector< Math::SpatialVector > | f_ext_constraints |
| Workspace for the actual spatial forces. More... | |
| std::vector< Math::Vector3d > | point_accel_0 |
| Workspace for the default point accelerations. More... | |
| std::vector< Math::SpatialVector > | d_pA |
| Workspace for the bias force due to the test force. More... | |
| std::vector< Math::SpatialVector > | d_a |
| Workspace for the acceleration due to the test force. More... | |
| Math::VectorNd | d_u |
| std::vector< Math::SpatialMatrix > | d_IA |
| Workspace for the inertia when applying constraint forces. More... | |
| std::vector< Math::SpatialVector > | d_U |
| Workspace when applying constraint forces. More... | |
| Math::VectorNd | d_d |
| Workspace when applying constraint forces. More... | |
| std::vector< Math::Vector3d > | d_multdof3_u |
| ConstraintCache | cache |
Detailed Description
Constraints are handled by specification of a ConstraintSet which contains all information about the current constraints and workspace memory.
Separate constraints can be specified by calling ConstraintSet::AddContactConstraint(), ConstraintSet::AddLoopConstraint(), and ConstraintSet::AddCustomConstraint(). After all constraints have been specified, this ConstraintSet has to be bound to the model via ConstraintSet::Bind(). This initializes workspace memory that is later used when calling one of the contact functions, such as ForwardDynamicsContactsDirects().
The values in the vectors ConstraintSet::force and ConstraintSet::impulse contain the Lagrange multipliers or change in Lagrange multipliers for each constraint when returning from one of the contact functions.
Solution of the Constraint System
Linear System of the Constrained Dynamics
In the presence of constraints, to compute the acceleration one has to solve a linear system of the form:
![\[ \left( \begin{array}{cc} H & G^T \\ G & 0 \end{array} \right) \left( \begin{array}{c} \ddot{q} \\ - \lambda \end{array} \right) = \left( \begin{array}{c} -C + \tau \\ \gamma \end{array} \right) \]](../../form_27.png)
where 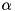 is the joint space inertia matrix computed with the CompositeRigidBodyAlgorithm(),
is the joint space inertia matrix computed with the CompositeRigidBodyAlgorithm(), 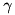 is the constraint Jacobian,
is the constraint Jacobian, 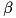 the bias force (sometimes called "non-linear
effects"), and
the bias force (sometimes called "non-linear
effects"), and 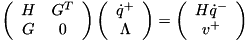 the generalized acceleration independent part of the constraints.
the generalized acceleration independent part of the constraints.
Linear System of the Constraint Impacts
Similarly to compute the response of the model to a constraint gain one has to solve a system of the following form:
![\[ \left( \begin{array}{cc} H & G^T \\ G & 0 \end{array} \right) \left( \begin{array}{c} \dot{q}^{+} \\ \Lambda \end{array} \right) = \left( \begin{array}{c} H \dot{q}^{-} \\ v^{+} \end{array} \right) \]](../../form_30.png)
where 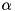 is the joint space inertia matrix computed with the CompositeRigidBodyAlgorithm(),
is the joint space inertia matrix computed with the CompositeRigidBodyAlgorithm(), 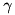 are the Jacobians of the constraints,
are the Jacobians of the constraints, 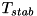 the generalized velocity after the impact,
the generalized velocity after the impact, 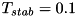 the impulses at each constraint,
the impulses at each constraint, 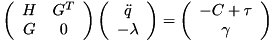 the generalized velocity before the impact, and
the generalized velocity before the impact, and 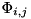 the desired velocity of each constraint after the impact (known beforehand, usually 0). The value of
the desired velocity of each constraint after the impact (known beforehand, usually 0). The value of 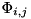 can is specified via the variable ConstraintSet::v_plus and defaults to 0.
can is specified via the variable ConstraintSet::v_plus and defaults to 0.
Solution Methods
There are essentially three different approaches to solve these systems:
- Direct: solve the full system to simultaneously compute
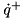 and
and 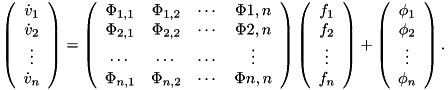 . This may be slow for large systems and many constraints.
. This may be slow for large systems and many constraints. - Range-Space: solve first for
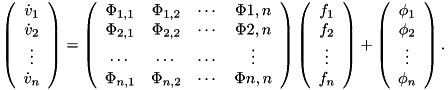 and then for
and then for  .
. - Null-Space: solve furst for
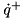 and then for
and then for  The methods are the same for the contact gains just with different variables on the right-hand-side.
The methods are the same for the contact gains just with different variables on the right-hand-side.
RBDL provides methods for all approaches. The implementation for the range-space method also exploits sparsities in the joint space inertia matrix using a sparse structure preserving 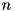 decomposition as described in Chapter 8.5 of "Rigid Body Dynamics Algorithms".
decomposition as described in Chapter 8.5 of "Rigid Body Dynamics Algorithms".
None of the methods is generally superior to the others and each has different trade-offs as factors such as model topology, number of constraints, constrained bodies, numerical stability, and performance vary and evaluation has to be made on a case-by-case basis.
Methods for Solving Constrained
Dynamics
RBDL provides the following methods to compute the acceleration of a constrained system:
- ForwardDynamicsConstraintsDirect()
- ForwardDynamicsConstraintsRangeSpaceSparse()
- ForwardDynamicsConstraintsNullSpace()
Methods for Computing Collisions
RBDL provides the following methods to compute the collision response on new contact gains:
- ComputeConstraintImpulsesDirect()
- ComputeConstraintImpulsesRangeSpaceSparse()
- ComputeConstraintImpulsesNullSpace()
Computing generalized joint positions and velocities
satisfying the constraint equations.
When considering a model subject position level constraints expressed by the equation 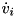 , it is often necessary to compute generalized joint position and velocities which satisfy the constraints. Even velocity-level constraints may have position-level assembly constraints: a rolling-without-slipping constraint is a velocity-level constraint, but during assembly it might be desireable to put the rolling surfaces in contact with eachother.
, it is often necessary to compute generalized joint position and velocities which satisfy the constraints. Even velocity-level constraints may have position-level assembly constraints: a rolling-without-slipping constraint is a velocity-level constraint, but during assembly it might be desireable to put the rolling surfaces in contact with eachother.
In order to compute a vector of generalized joint positions that satisfy the constraints it is necessary to solve the following optimization problem:
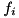
In order to compute a vector of generalized joint velocities that satisfy the constraints it is necessary to solve the following optimization problem:
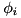
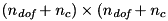 and
and 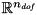 are initial guesses,
are initial guesses, 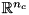 is the constraints Jacobian (partial derivative of
is the constraints Jacobian (partial derivative of 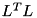 with respect to
with respect to 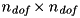 ), and
), and 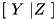 is the partial derivative of
is the partial derivative of 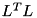 with respect to time.
with respect to time. 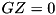 is a diagonal weighting matrix, which can be exploited to prioritize changes in the position/ velocity of specific joints. With a solver capable of handling singular matrices, it is possible to set to 1 the weight of the joint positions/ velocities that should not be changed from the initial guesses, and to 0 those corresponding to the values that can be changed.
is a diagonal weighting matrix, which can be exploited to prioritize changes in the position/ velocity of specific joints. With a solver capable of handling singular matrices, it is possible to set to 1 the weight of the joint positions/ velocities that should not be changed from the initial guesses, and to 0 those corresponding to the values that can be changed.
These problems are solved using the Lagrange multipliers method. For the velocity problem the solution is exact. For the position problem the constraints are linearized in the form 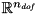 and the linearized problem is solved iteratively until the constraint position errors are smaller than a given threshold.
and the linearized problem is solved iteratively until the constraint position errors are smaller than a given threshold.
RBDL provides two functions to compute feasible joint position and velocities:
Baumgarte Stabilization
The constrained dynamic equations are correct at the acceleration level but will drift at the velocity and position level during numerical integration. RBDL implements Baumgarte stabilization to avoid the accumulation of position and velocity errors for loop constraints and custom constraints. Contact constraints do not have Baumgarte stabilization because they are a special case which does not typically suffer from drift. The stabilization term can be enabled/disabled using the appropriate ConstraintSet::AddLoopConstraint and ConstraintSet::AddCustomConstraint functions.
The dynamic equations are changed to the following form:
![\[ \left( \begin{array}{cc} H & G^T \\ G & 0 \end{array} \right) \left( \begin{array}{c} \ddot{q} \\ - \lambda \end{array} \right) = \left( \begin{array}{c} -C + \tau \\ \gamma + \gamma _{stab} \end{array} \right) \]](../../form_48.png)
A term 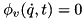 is added to the right hand side of the equation, defined in the following way:
is added to the right hand side of the equation, defined in the following way:
![\[ \gamma _{stab} = - 2 \alpha \dot{\phi} (q) - \beta^2 \phi (q) \]](../../form_50.png)
where 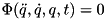 are the position level constraint errors and
are the position level constraint errors and 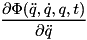 and
and 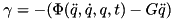 are tuning coefficients. There is no clear and simple rule on how to choose them as good values also depend on the used integration method and time step. If the values are too small the constrained dynamics equation becomes stiff, too big values result in errors not being reduced.
are tuning coefficients. There is no clear and simple rule on how to choose them as good values also depend on the used integration method and time step. If the values are too small the constrained dynamics equation becomes stiff, too big values result in errors not being reduced.
A good starting point is to parameterize the coefficients as:
![\[ \alpha = \beta = 1 / T_\textit{stab} \]](../../form_54.png)
with 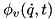 specifies a time constant for errors in position and velocity errors to reduce. Featherstone suggests in his book "Rigid
Body Dynamics Algorithms" that for a big industrial robot a value of 0.1 is reasonable. When testing different values best is to try different orders of magnitude as e.g. doubling a value only has little effect.
specifies a time constant for errors in position and velocity errors to reduce. Featherstone suggests in his book "Rigid
Body Dynamics Algorithms" that for a big industrial robot a value of 0.1 is reasonable. When testing different values best is to try different orders of magnitude as e.g. doubling a value only has little effect.
FBaumgarte stabilization is disabled by default, and uses the default the stabilization parameter 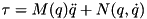 .
.
Function Documentation
◆ ConstraintSet()
|
inline |
Definition at line 282 of file Constraints.h.
◆ AddContactConstraint()
| unsigned int AddContactConstraint | ( | unsigned int | bodyId, |
| const Math::Vector3d & | bodyPoint, | ||
| const Math::Vector3d & | worldNormal, | ||
| const char * | constraintName = NULL, |
||
| unsigned int | userDefinedId = std::numeric_limits< unsigned int >::max() |
||
| ) |
Adds a single contact constraint (point-ground) to the constraint set.
This type of constraints ensures that the velocity and acceleration of a specified body point along a specified axis are null.
- Parameters
-
bodyId the body which is affected directly by the constraint bodyPoint the point that is constrained relative to the contact body worldNormal the normal direction in which to apply the constraint constraintName a human readable name (optional, default: NULL). Set this field to a unique name (within this ConstraintSet) so that the function GetConstraintIndex can find it. userDefinedId a user defined id (optional, defaults to max()). Set this field to a unique number (within this ConstraintSet) so that the function GetConstraintIndex can find it.
◆ AddCustomConstraint()
| unsigned int AddCustomConstraint | ( | std::shared_ptr< Constraint > | customConstraint | ) |
Adds a custom constraint to the constraint set.
- Parameters
-
customConstraint The CustomConstraint to be added to the ConstraintSet
◆ AddLoopConstraint()
| unsigned int AddLoopConstraint | ( | unsigned int | bodyIdPredecessor, |
| unsigned int | bodyIdSuccessor, | ||
| const Math::SpatialTransform & | XPredecessor, | ||
| const Math::SpatialTransform & | XSuccessor, | ||
| const Math::SpatialVector & | constraintAxisInPredecessor, | ||
| bool | enableBaumgarteStabilization = false, |
||
| double | stabilizationTimeConstant = 0.1, |
||
| const char * | constraintName = NULL, |
||
| unsigned int | userDefinedId = std::numeric_limits< unsigned int >::max() |
||
| ) |
Adds a loop constraint to the constraint set.
This type of constraints ensures that the relative orientation and position, spatial velocity, and spatial acceleration between two frames in two bodies are null along a specified spatial constraint axis.
- Parameters
-
bodyIdPredecessor the identifier of the predecessor body bodyIdSuccessor the identifier of the successor body XPredecessor a spatial transform localizing the constrained frames on the predecessor body, expressed with respect to the predecessor body frame. Note the position vector should be the r_BPB (from the body's origin, to the predessor frame, in the coordinates of the body's frame) and E_BP (the rotation matrix that will rotate vectors from the coordinates of the P frame to the coordinates of the body's frame). XSuccessor a spatial transform localizing the constrained frames on the successor body, expressed with respect to the successor body frame. Note the position vector should be the r_BSB (from the body's origin, to the successor frame, in the coordinates of the body's frame) and E_BS (the rotation matrix that will rotate vectors from the coordinates of the S frame to the coordinates of the body's frame). constraintAxisInPredecessor a spatial vector, resolved in the frame of the predecessor frame, indicating the axis along which the constraint acts enableBaumgarteStabilization (optional, default false) setting this flag to true will modify the right hand side of the acceleration equation with a penaltiy term that is proportional to the constraint error scaled by a constant. stabilizationTimeConstant (optional, defaults to 0.1 sec) this value scales the strength of Baumgarte stabilization so that the settling time of the error is proportional the value given here. constraintName a human readable name (optional, default: NULL). Set this field to a unique name (within this ConstraintSet) so that the function GetConstraintIndex can find it. userDefinedId a user defined id (optional, defaults to max()). Set this field to a unique number (within this ConstraintSet) so that the function GetConstraintIndex can find it.
◆ Bind()
| bool Bind | ( | const Model & | model | ) |
Initializes and allocates memory for the constraint set.
This function allocates memory for temporary values and matrices that are required for contact force computation. Both model and constraint set must not be changed after a binding as the required memory is dependent on the model size (i.e. the number of bodies and degrees of freedom) and the number of constraints in the Constraint set.
The values of ConstraintSet::acceleration may still be modified after the set is bound to the model.
◆ CalcAssemblyQ()
| RBDL_DLLAPI bool RigidBodyDynamics::CalcAssemblyQ | ( | Model & | model, |
| Math::VectorNd | QInit, | ||
| ConstraintSet & | CS, | ||
| Math::VectorNd & | QOutput, | ||
| const Math::VectorNd & | weights, | ||
| double | tolerance = 1e-12, |
||
| unsigned int | max_iter = 100 |
||
| ) |
Computes a feasible initial value of the generalized joint positions.
- Parameters
-
model the model QInit initial guess for the generalized positions of the joints CS the constraint set for which the error should be computed QOutput vector of the generalized joint positions. weights weighting coefficients for the different joint positions. tolerance the function will return successfully if the constraint position error norm is lower than this value. max_iter the funciton will return unsuccessfully after performing this number of iterations.
- Returns
- true if the generalized joint positions were computed successfully, false otherwise.f
◆ CalcAssemblyQDot()
| RBDL_DLLAPI void RigidBodyDynamics::CalcAssemblyQDot | ( | Model & | model, |
| const Math::VectorNd & | Q, | ||
| const Math::VectorNd & | QDotInit, | ||
| ConstraintSet & | CS, | ||
| Math::VectorNd & | QDotOutput, | ||
| const Math::VectorNd & | weights | ||
| ) |
Computes a feasible initial value of the generalized joint velocities.
- Parameters
-
model the model Q the generalized joint position of the joints. It is assumed that this vector satisfies the position level assemblt constraints. QDotInit initial guess for the generalized velocities of the joints CS the constraint set for which the error should be computed QDotOutput vector of the generalized joint velocities. weights weighting coefficients for the different joint positions.
◆ calcBaumgarteStabilizationForces()
| void calcBaumgarteStabilizationForces | ( | unsigned int | groupIndex, |
| Model & | model, | ||
| const Math::VectorNd & | positionError, | ||
| const Math::VectorNd & | velocityError, | ||
| Math::VectorNd & | baumgarteForcesOutput | ||
| ) |
- Parameters
-
groupIndex the index number of this constraint (see getGroupIndex index functions) model the multibody model positionError the position errors associated with this constraint computed using the calcConstraintPositionError function velocityError the velocity errors associated with this constraint computed using the calcConstraintVelocityError function baumgarteForcesOutput (output) a reference to the vector of baumgarte stabilization forces applied to this this constraint.
◆ CalcConstrainedSystemVariables()
| RBDL_DLLAPI void RigidBodyDynamics::CalcConstrainedSystemVariables | ( | Model & | model, |
| const Math::VectorNd & | Q, | ||
| const Math::VectorNd & | QDot, | ||
| const Math::VectorNd & | Tau, | ||
| ConstraintSet & | CSOutput, | ||
| bool | update_kinematics = true, |
||
| std::vector< Math::SpatialVector > * | f_ext = NULL |
||
| ) |
Computes the terms 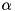 ,
, 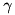 , and
, and 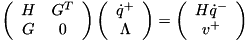 of the constrained dynamic problem and stores them in the ConstraintSet.
of the constrained dynamic problem and stores them in the ConstraintSet.
- Parameters
-
model the model Q the generalized positions of the joints QDot the generalized velocities of the joints Tau the generalized forces of the joints CSOutput the constraint set for which the error should be computed update_kinematics whether the kinematics of the model should be updated from Q. f_ext External forces acting on the body in base coordinates (optional, defaults to NULL)
- Note
- This function is normally called automatically in the various constrained dynamics functions, the user normally does not have to call it.
◆ CalcConstraintsJacobian()
| RBDL_DLLAPI void RigidBodyDynamics::CalcConstraintsJacobian | ( | Model & | model, |
| const Math::VectorNd & | Q, | ||
| ConstraintSet & | CS, | ||
| Math::MatrixNd & | GOutput, | ||
| bool | update_kinematics = true |
||
| ) |
Computes the Jacobian for the given ConstraintSet.
- Parameters
-
model the model Q the generalized positions of the joints CS the constraint set for which the Jacobian should be computed GOutput matrix where the output will be stored in update_kinematics whether the kinematics of the model should be updated from Q
◆ CalcConstraintsPositionError()
| RBDL_DLLAPI void RigidBodyDynamics::CalcConstraintsPositionError | ( | Model & | model, |
| const Math::VectorNd & | Q, | ||
| ConstraintSet & | CS, | ||
| Math::VectorNd & | errOutput, | ||
| bool | update_kinematics = true |
||
| ) |
Computes the position errors for the given ConstraintSet.
- Parameters
-
model the model Q the generalized positions of the joints CS the constraint set for which the error should be computed errOutput vector where the error will be stored in (should have the size of CS). update_kinematics whether the kinematics of the model should be updated from Q.
- Note
- the position error is always 0 for contact constraints.
◆ CalcConstraintsVelocityError()
| RBDL_DLLAPI void RigidBodyDynamics::CalcConstraintsVelocityError | ( | Model & | model, |
| const Math::VectorNd & | Q, | ||
| const Math::VectorNd & | QDot, | ||
| ConstraintSet & | CS, | ||
| Math::VectorNd & | errOutput, | ||
| bool | update_kinematics = true |
||
| ) |
Computes the velocity errors for the given ConstraintSet.
- Parameters
-
model the model Q the generalized positions of the joints QDot the generalized velocities of the joints CS the constraint set for which the error should be computed errOutput vector where the error will be stored in (should have the size of CS). update_kinematics whether the kinematics of the model should be updated from Q.
- Note
- this is equivalent to multiplying the constraint Jacobian by the generalized velocities of the joints.
◆ calcForces()
| void calcForces | ( | unsigned int | groupIndex, |
| Model & | model, | ||
| const Math::VectorNd & | Q, | ||
| const Math::VectorNd & | QDot, | ||
| std::vector< unsigned int > & | updConstraintBodyIdsOutput, | ||
| std::vector< Math::SpatialTransform > & | updConstraintBodyFramesOutput, | ||
| std::vector< Math::SpatialVector > & | updConstraintForcesOutput, | ||
| bool | resolveAllInRootFrame = false, |
||
| bool | updateKinematics = false |
||
| ) |
calcForces resolves the generalized forces generated by this constraint into equivalent spatial forces (resolved in the local or the base frame) that are applied between the bodies and frames that this constraint applies to.
- Note
- Important: The values returned by this function are only valid after one of the dynamics methods (ForwardDynamicsConstraintsDirect, ForwardDynamicsConstraintsNullSpace, InverseDynamicsWithConstraints, etc) have been evaluated. Why? This function makes use of the Lagrange multipliers which are only evaluated when these dynamics-level functions are called.
- Parameters
-
groupIndex the index number of this constraint (see getGroupIndex index functions) model the multibody model Q the generalized positions of the model QDot the generalized velocities of the model constraintBodyIdsOutputUpd a reference to a vector of body ids in which the spatial forces are resolved into. The ordering for the standard constraints are as follows : - ContactConstraint
- [0] : body
- [1] : ground
- Loop Constraint
- [0] : predecessor body
- [1] : successor
constraintBodyFramesOutputUpd a reference to a vector of frames in which the spatial forces are resolved. The 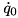 frame is located in the
frame is located in the 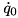 body id listed in constraintBodyIdsOutput.
body id listed in constraintBodyIdsOutput.constraintForcesOutputUpd a reference to a vector of spatial forces generated by this constraint. The 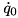 spatial force is resolved into the
spatial force is resolved into the 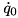 frame listed in constraintBodyFramesOutput.
frame listed in constraintBodyFramesOutput.resolveAllInRootFrame - false: spatial forces are resolved into the local frames attached to the bodies involved in this constraint
- true: spatial forces are resolved into the base frame. Note that this means that all entires in constraintBodyIdsOutput will be 0, the frames in constraintFramesOutput will have their origins at the contact frames but with directions that match the base frame.
updateKinematics setting this flag to true will trigger the kinematic transforms of the model to be updated. - ContactConstraint
◆ calcImpulses()
| void calcImpulses | ( | unsigned int | groupIndex, |
| Model & | model, | ||
| const Math::VectorNd & | Q, | ||
| const Math::VectorNd & | QDot, | ||
| std::vector< unsigned int > & | constraintBodyIdsOutput, | ||
| std::vector< Math::SpatialTransform > & | constraintBodyFramesOutput, | ||
| std::vector< Math::SpatialVector > & | constraintImpulsesOutput, | ||
| bool | resolveAllInRootFrame = false, |
||
| bool | updateKinematics = false |
||
| ) |
calcImpulses resolves the generalized impluses generated by this constraint into equivalent spatial impulses (resolved in the local or the base frame) that are applied between the bodies and frames that this constraint applies to.
- Note
- Important: The values returned by this function are only valid after one of the impulse methods (ComputeConstraintImpulsesDirect, ComputeConstraintImpulsesNullSpace, etc) have been evaluated. Why? This function makes use of the Lagrange multipliers which are only evaluated when these dynamics-level functions are called.
- Parameters
-
groupIndex the index number of this constraint (see getGroupIndex index functions) model the multibody model Q the generalized positions of the model QDot the generalized velocities of the model constraintBodyIdsOutput a vector of body ids in which the spatial forces are resolved into. The ordering for the standard constraints are as follows : - ContactConstraint
- [0] : body
- [1] : ground
- Loop Constraint
- [0] : predecessor body
- [1] : successor
constraintBodyFramesOutput a vector of frames in which the spatial forces are resolved. The 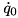 frame is located in the
frame is located in the 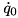 body id listed in constraintBodyIdsOutput.
body id listed in constraintBodyIdsOutput.constraintImpulsesOutput a vector of spatial impulses generated by this constraint. The 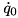 spatial impulse is resolved into the
spatial impulse is resolved into the 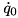 frame listed in constraintBodyFramesOutput.
frame listed in constraintBodyFramesOutput.resolveAllInRootFrame - false: spatial impulses are resolved into the local frames attached to the bodies involved in this constraint
- true: spatial impulses are resolved into the base frame. Note that this means that all entires in constraintBodyIdsOutput will be 0, the frames in constraintFramesOutput will have their origins at the contact frames but with directions that match the base frame.
updateKinematics setting this flag to true will trigger the kinematic transforms of the model to be updated. - ContactConstraint
◆ calcPositionError()
| void calcPositionError | ( | unsigned int | groupIndex, |
| Model & | model, | ||
| const Math::VectorNd & | Q, | ||
| Math::VectorNd & | positionErrorOutput, | ||
| bool | updateKinematics = false |
||
| ) |
calcPositionError calculates the vector of position errors associated with this constraint. Note that if the constraint group, or parts of it, are not defined at the position level then 0's will be returned.
- Parameters
-
groupIndex the index number of this constraint (see getGroupIndex index functions) model the multibody model Q the generalized positions of the model positionErrorOutput (output) a reference to the vector of constraint errors updateKinematics setting this flag to true will trigger the kinematic transforms of the model to be updated.
◆ calcVelocityError()
| void calcVelocityError | ( | unsigned int | groupIndex, |
| Model & | model, | ||
| const Math::VectorNd & | Q, | ||
| const Math::VectorNd & | QDot, | ||
| Math::VectorNd & | velocityErrorOutput, | ||
| bool | updateKinematics = false |
||
| ) |
calcVelocityError calculates the vector of position errors associated with this constraint. Note that if the constraint group, or parts of it, are not defined at the position level then 0's will be returned.
- Parameters
-
groupIndex the index number of this constraint (see getGroupIndex index functions) model the multibody model Q the generalized positions of the model QDot the generalized velocities of the model velocityErrorOutput (output) the vector of constraint errors at the velocity level updateKinematics setting this flag to true will trigger the kinematic transforms of the model to be updated.
◆ clear()
| void clear | ( | ) |
Clears all variables in the constraint set.
◆ ComputeConstraintImpulsesDirect()
| RBDL_DLLAPI void RigidBodyDynamics::ComputeConstraintImpulsesDirect | ( | Model & | model, |
| const Math::VectorNd & | Q, | ||
| const Math::VectorNd & | QDotMinus, | ||
| ConstraintSet & | CS, | ||
| Math::VectorNd & | QDotPlusOutput | ||
| ) |
Computes contact gain by constructing and solving the full lagrangian equation.
This method builds and solves the linear system
![\[ \left( \begin{array}{cc} H & G^T \\ G & 0 \end{array} \right) \left( \begin{array}{c} \dot{q}^{+} \\ \Lambda \end{array} \right) = \left( \begin{array}{c} H \dot{q}^{-} \\ v^{+} \end{array} \right) \]](../../form_30.png)
where 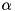 is the joint space inertia matrix computed with the CompositeRigidBodyAlgorithm(),
is the joint space inertia matrix computed with the CompositeRigidBodyAlgorithm(), 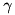 are the point Jacobians of the contact points,
are the point Jacobians of the contact points, 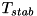 the generalized velocity after the impact,
the generalized velocity after the impact, 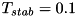 the impulses at each constraint,
the impulses at each constraint, 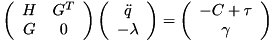 the generalized velocity before the impact, and
the generalized velocity before the impact, and 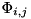 the desired velocity of each constraint after the impact (known beforehand, usually 0). The value of
the desired velocity of each constraint after the impact (known beforehand, usually 0). The value of 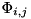 can is specified via the variable ConstraintSet::v_plus and defaults to 0.
can is specified via the variable ConstraintSet::v_plus and defaults to 0.
- Note
- So far, only constraints acting along cartesian coordinate axes are allowed (i.e. (1, 0, 0), (0, 1, 0), and (0, 0, 1)). Also, one must not specify redundant constraints!
- Note
- To increase performance group constraints body and pointwise such that constraints acting on the same body point are sequentially in ConstraintSet. This can save computation of point Jacobians
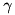 .
.
- Parameters
-
model rigid body model Q state vector of the internal joints QDotMinus velocity vector of the internal joints before the impact CS the set of active constraints QDotPlusOutput velocities of the internals joints after the impact
◆ ComputeConstraintImpulsesNullSpace()
| RBDL_DLLAPI void RigidBodyDynamics::ComputeConstraintImpulsesNullSpace | ( | Model & | model, |
| const Math::VectorNd & | Q, | ||
| const Math::VectorNd & | QDotMinus, | ||
| ConstraintSet & | CS, | ||
| Math::VectorNd & | QDotPlusOutput | ||
| ) |
Resolves contact gain using SolveContactSystemNullSpace()
- Parameters
-
model rigid body model Q state vector of the internal joints QDotMinus velocity vector of the internal joints before the impact CS the set of active constraints QDotPlusOutput velocities of the internals joints after the impact
◆ ComputeConstraintImpulsesRangeSpaceSparse()
| RBDL_DLLAPI void RigidBodyDynamics::ComputeConstraintImpulsesRangeSpaceSparse | ( | Model & | model, |
| const Math::VectorNd & | Q, | ||
| const Math::VectorNd & | QDotMinus, | ||
| ConstraintSet & | CS, | ||
| Math::VectorNd & | QDotPlusOutput | ||
| ) |
Resolves contact gain using SolveContactSystemRangeSpaceSparse()
- Parameters
-
model rigid body model Q state vector of the internal joints QDotMinus velocity vector of the internal joints before the impact CS the set of active constraints QDotPlusOutput velocities of the internals joints after the impact
◆ Copy()
|
inline |
Copies the constraints and resets its ConstraintSet::bound flag.
Definition at line 798 of file Constraints.h.
References ConstraintSet::bound.
◆ disableBaumgarteStabilization()
|
inline |
- Parameters
-
groupIndex the index number of this constraint (see getGroupIndex index functions)
Definition at line 681 of file Constraints.h.
◆ enableBaumgarteStabilization()
|
inline |
- Parameters
-
groupIndex the index number of this constraint (see getGroupIndex index functions)
Definition at line 672 of file Constraints.h.
◆ ForwardDynamicsConstraintsDirect()
| RBDL_DLLAPI void RigidBodyDynamics::ForwardDynamicsConstraintsDirect | ( | Model & | model, |
| const Math::VectorNd & | Q, | ||
| const Math::VectorNd & | QDot, | ||
| const Math::VectorNd & | Tau, | ||
| ConstraintSet & | CS, | ||
| Math::VectorNd & | QDDotOutput, | ||
| bool | update_kinematics = true, |
||
| std::vector< Math::SpatialVector > * | f_ext = NULL |
||
| ) |
Computes forward dynamics with contact by constructing and solving the full lagrangian equation.
This method builds and solves the linear system
![\[ \left( \begin{array}{cc} H & G^T \\ G & 0 \end{array} \right) \left( \begin{array}{c} \ddot{q} \\ -\lambda \end{array} \right) = \left( \begin{array}{c} -C + \tau \\ \gamma \end{array} \right) \]](../../form_57.png)
where 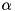 is the joint space inertia matrix computed with the CompositeRigidBodyAlgorithm(),
is the joint space inertia matrix computed with the CompositeRigidBodyAlgorithm(), 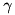 are the point Jacobians of the contact points,
are the point Jacobians of the contact points, 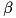 the bias force (sometimes called "non-linear
effects"), and
the bias force (sometimes called "non-linear
effects"), and 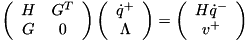 the generalized acceleration independent part of the contact point accelerations.
the generalized acceleration independent part of the contact point accelerations.
- Note
- This function works with ContactConstraints, LoopConstraints and Custom Constraints. Nonetheless, this method will not tolerate redundant constraints.
- Note
- To increase performance group constraints body and pointwise such that constraints acting on the same body point are sequentially in ConstraintSet. This can save computation of point Jacobians
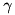 .
.
- Parameters
-
model rigid body model Q state vector of the internal joints QDot velocity vector of the internal joints Tau actuations of the internal joints CS the description of all acting constraints QDDotOutput accelerations of the internals joints update_kinematics whether the kinematics of the model should be updated from Q. f_ext External forces acting on the body in base coordinates (optional, defaults to NULL)
- Note
- During execution of this function values such as ConstraintSet::force get modified and will contain the value of the force acting along the normal.
◆ ForwardDynamicsConstraintsNullSpace()
| RBDL_DLLAPI void RigidBodyDynamics::ForwardDynamicsConstraintsNullSpace | ( | Model & | model, |
| const Math::VectorNd & | Q, | ||
| const Math::VectorNd & | QDot, | ||
| const Math::VectorNd & | Tau, | ||
| ConstraintSet & | CS, | ||
| Math::VectorNd & | QDDotOutput, | ||
| bool | update_kinematics = true, |
||
| std::vector< Math::SpatialVector > * | f_ext = NULL |
||
| ) |
◆ ForwardDynamicsConstraintsRangeSpaceSparse()
| RBDL_DLLAPI void RigidBodyDynamics::ForwardDynamicsConstraintsRangeSpaceSparse | ( | Model & | model, |
| const Math::VectorNd & | Q, | ||
| const Math::VectorNd & | QDot, | ||
| const Math::VectorNd & | Tau, | ||
| ConstraintSet & | CS, | ||
| Math::VectorNd & | QDDotOutput, | ||
| bool | update_kinematics = true, |
||
| std::vector< Math::SpatialVector > * | f_ext = NULL |
||
| ) |
◆ ForwardDynamicsContactsKokkevis()
| RBDL_DLLAPI void RigidBodyDynamics::ForwardDynamicsContactsKokkevis | ( | Model & | model, |
| const Math::VectorNd & | Q, | ||
| const Math::VectorNd & | QDot, | ||
| const Math::VectorNd & | Tau, | ||
| ConstraintSet & | CS, | ||
| Math::VectorNd & | QDDotOutput | ||
| ) |
Computes forward dynamics that accounts for active contacts in ConstraintSet.
The method used here is the one described by Kokkevis and Metaxas in the Paper "Practical Physics for Articulated Characters", Game Developers Conference, 2004.
It does this by recursively computing the inverse articulated-body inertia (IABI) 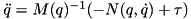 which is then used to build and solve a system of the form:
which is then used to build and solve a system of the form:
![\[ \left( \begin{array}{c} \dot{v}_1 \\ \dot{v}_2 \\ \vdots \\ \dot{v}_n \end{array} \right) = \left( \begin{array}{cccc} \Phi_{1,1} & \Phi_{1,2} & \cdots & \Phi{1,n} \\ \Phi_{2,1} & \Phi_{2,2} & \cdots & \Phi{2,n} \\ \cdots & \cdots & \cdots & \vdots \\ \Phi_{n,1} & \Phi_{n,2} & \cdots & \Phi{n,n} \end{array} \right) \left( \begin{array}{c} f_1 \\ f_2 \\ \vdots \\ f_n \end{array} \right) + \left( \begin{array}{c} \phi_1 \\ \phi_2 \\ \vdots \\ \phi_n \end{array} \right). \]](../../form_59.png)
Here 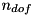 is the number of constraints and the method for building the system uses the Articulated Body Algorithm to efficiently compute entries of the system. The values
is the number of constraints and the method for building the system uses the Articulated Body Algorithm to efficiently compute entries of the system. The values 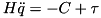 are the constraint accelerations,
are the constraint accelerations, 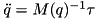 the constraint forces, and
the constraint forces, and 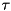 are the constraint bias forces.
are the constraint bias forces.
- Parameters
-
model rigid body model Q state vector of the internal joints QDot velocity vector of the internal joints Tau actuations of the internal joints CS a list of all contact points QDDotOutput accelerations of the internals joints
- Note
- During execution of this function values such as ConstraintSet::force get modified and will contain the value of the force acting along the normal.
- This function supports only contact constraints.
- Todo:
- Allow for external forces
◆ getBaumgarteStabilizationCoefficients()
|
inline |
Definition at line 687 of file Constraints.h.
◆ getGroupAssignedId()
|
inline |
Returns assigned id of the constraint group which will be the first id assigned to an entry in a group (if the grouping was done automatically - as is done for contact and loop constraints).
- Parameters
-
groupIndex the index number of a constraint group.
- Returns
- the assigned of the constraint group. For constraints that are grouped automatically (e.g. contact and loop constraints) the assigned id will be the assigned id fo the of the first constraint added to the group. For constraints which are not automatically grouped (e.g. CustomConstraints) the assigned id is identical to the one returned when the constraint was added to the constraint set (e.g. when AddCustomConstraint was called).
Definition at line 432 of file Constraints.h.
◆ getGroupId()
|
inline |
Returns the user-defined-id of the constraint group, which may differ from the names entered by the user if the constraint is one in which grouping is done automatically (e.g. contact and loop constraints).
- Parameters
-
groupIndex the index number of a constraint group.
- Returns
- the user-defined-id of the constraint group. For constraints that are grouped automatically (e.g. contact and loop constraints) the user-defined-id will be the user-defined-id fo the of the first constraint added to the group. For constraints which are not automatically grouped (e.g. CustomConstraints) the user-defined-id is identical to the one the user assigned (optionally) when the constraint was added to the constraint set (e.g. when AddCustomConstraint was called).
Definition at line 411 of file Constraints.h.
◆ getGroupIndexByAssignedId()
|
inline |
getGroupIndex returns the index to a constraints that have been grouped because they are of the same type, apply to the same bodies, and apply to the same local frames on each body.
- Parameters
-
assignedId : the integer id that was returned when the constraint was added to the constraint set by the functions: AddContactConstraint, AddLoopConstraint, AddCustomConstraint, etc.
- Returns
- : the group index of the constraint
Definition at line 337 of file Constraints.h.
◆ getGroupIndexById()
|
inline |
getGroupIndex returns the index to a constraints that have been grouped because they are of the same type, apply to the same bodies, and apply to the same local frames on each body.
- Parameters
-
userDefinedId : the optional integer id that was assigned to this constraint when it was created.
- Returns
- : the group index of the constraint
Definition at line 320 of file Constraints.h.
◆ getGroupIndexByName()
|
inline |
getGroupIndex returns the index to a constraints that have been grouped because they are of the same type, apply to the same bodies, and apply to the same local frames on each body.
- Note
- Internally this function makes a temporary string. If speed is a concern then do not call this function in a loop: either save the index locally, use the userDefinedId (which is an integer), or use the assigned id (also an integer).
- Parameters
-
userDefinedName : the optional name that the constraint was assigned when it was added to the constraint set.
- Returns
- : the group index of the constraint
Definition at line 304 of file Constraints.h.
◆ getGroupIndexMax()
|
inline |
getGroupIndexMax returns the maximum valid constraint group index (the min. is zero) so that constraint groups can be iterated over if desired.
- Returns
- the largest group index
Definition at line 348 of file Constraints.h.
◆ getGroupName()
|
inline |
Returns the name of the constraint group, which may differ from the names entered by the user if the constraint is one in which grouping is done automatically (e.g. contact and loop constraints)
- Parameters
-
groupIndex the index number of a constraint group.
- Returns
- the name of the constraint group. For constraints that are grouped automatically (e.g. contact and loop constraints) the group name is the name of the first constraint added to the group. For constraints which are not automatically grouped (e.g. CustomConstraints) the group name is identical to the optional name used when the constraint was added to the constraint set (e.g. when AddCustomConstraint was called).
Definition at line 368 of file Constraints.h.
◆ getGroupSize()
|
inline |
Returns the number of constraint equations in this group.
- Parameters
-
groupIndex the index number of a constraint group.
- Returns
- the number of constraint equations in this group. If this is a constraint where constraints are automatically grouped (e.g. contact and loop constraints) the size might be larger than you expect.
Definition at line 380 of file Constraints.h.
◆ getGroupType()
|
inline |
Returns integer corresponding to the ConstraintType.
- Parameters
-
groupIndex the index number of a constraint group.
- Returns
- the integer that corresponds to the ConstraintType of this constraint group.
Definition at line 390 of file Constraints.h.
◆ InverseDynamicsConstraints()
| RBDL_DLLAPI void RigidBodyDynamics::InverseDynamicsConstraints | ( | Model & | model, |
| const Math::VectorNd & | Q, | ||
| const Math::VectorNd & | QDot, | ||
| const Math::VectorNd & | QDDotDesired, | ||
| ConstraintSet & | CS, | ||
| Math::VectorNd & | QDDotOutput, | ||
| Math::VectorNd & | TauOutput, | ||
| bool | update_kinematics = true, |
||
| std::vector< Math::SpatialVector > * | f_ext = NULL |
||
| ) |
An inverse-dynamics operator that can be applied to fully-actuated constrained systems.
- Important
- Set the actuated degrees-of-freedom using RigidBodyDynamics::ConstraintSet::SetActuationMap prior to calling this function.
- Use the function RigidBodyDynamics::isConstrainedSystemFullyActuated to determine if a system is fully actuated or not.
- This function implements an inverse-dynamics operator defined by Koch (1) (described in Eqn. 5.20) that can be applied to fully-actuated constraint systems and will solve for a set of physically-consistent
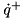 and
and 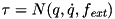 given a desired
given a desired  .
.
- To see test if a constrained system is fully actuated please use the function RigidBodyDynamics::isConstrainedSystemFullyActuated. If the constrained system is not fully actuated then the method RigidBodyDynamics::InverseDynamicsConstraintsRelaxed must be used instead.
- For a detailed explanation of the systems which cause this method to fail please read the text following Eqn. 5.20 in Koch's thesis, and the example that is given in Sec. 3 on pg 66. A brief summary is presented below.
- To begin,the generalized accelerations are partitioned into actuated parts
 and unactuated parts
and unactuated parts 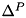
where![\[ u = S \ddot{q} \]](../../form_124.png)
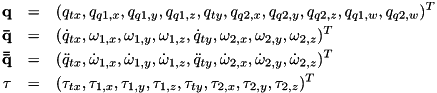 is an
is an 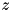 (number of actuated degrees-of-freedom) by
(number of actuated degrees-of-freedom) by 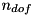 (number of degrees of freedom of the unconstrained system) selection matrix that picks out the actuated indices in
(number of degrees of freedom of the unconstrained system) selection matrix that picks out the actuated indices in 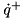 and
and
where![\[ v = P \ddot{q} \]](../../form_125.png)
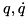 is an
is an 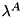 (number of unactuated degrees-of-freedom) by
(number of unactuated degrees-of-freedom) by 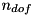 selection matrix that picks out the unactuated indices in
selection matrix that picks out the unactuated indices in 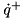 . By construction
. By construction
and thus![\[ \left(\begin{array}{cc} PP^T & 0 \\ 0 & SS^T \end{array}\right) = I_{n} \]](../../form_127.png)
We begin by projecting the constrained equations of motion![\[ \ddot{q} = S u + P v \]](../../form_128.png)
and adding the constraint that![\[ \left( \begin{array}{cc} H & G^T \\ G & 0 \end{array} \right) \left( \begin{array}{c} \ddot{q} \\ -\lambda \end{array} \right) =\left( \begin{array}{c} \tau - C\\ \gamma \end{array} \right) \]](../../form_129.png)
where![\[ u - S \ddot{q}^* = 0 \]](../../form_130.png)
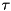 is a vector of desired accelerations. By considering only forces that are applied to the actuated parts (that is
is a vector of desired accelerations. By considering only forces that are applied to the actuated parts (that is 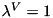 ) we can rearrange the system of equations
) we can rearrange the system of equations
By projecting this onto the onto the![\[ \left( \begin{array}{ccc} H & G^T & S^T\\ G & 0 & 0 \\ S & 0 & 0 \\ \end{array} \right) \left( \begin{array}{c} \ddot{q} \\ -\lambda \\ -\tau \end{array} \right) =\left( \begin{array}{c} - C\\ \gamma \\ S\ddot{q}^* \end{array} \right) \]](../../form_132.png)
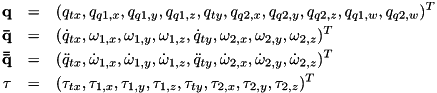 and
and 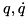 spaces
spaces
it becomes clear that this system of equations will be singular if![\[ \left( \begin{array}{cccc} S H S^T & S M P^T & S G^T & I \\ P M S^T & P M P^T & P G^T & 0\\ G S^T & G P^T & 0 & 0 \\ I & 0 & 0 & 0 \\ \end{array} \right) \left( \begin{array}{c} u \\ v \\ -\lambda\\ -\tau \end{array} \right) = \left( \begin{array}{c} -SC\\ -PC\\ \gamma\\ S \ddot{q}^* \end{array} \right) \]](../../form_133.png)
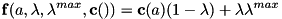 loses rank. Thus this method is appropriate to use provided that
loses rank. Thus this method is appropriate to use provided that
The implementation exploits the triangular structure of the matrix which means that only two linear systems of size![\[ \text{rank}( GP^T ) = n - n_a. \]](../../form_135.png)
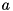 and
and 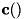 are performed which is much faster than solving the
are performed which is much faster than solving the 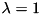 KKT matrix directly.
KKT matrix directly.
References
- Koch KH (2015). Using model-based optimal control for conceptional motion generation for the humannoid robot hrp-2 and design investigations for exo-skeletons. Heidelberg University (Doctoral dissertation).
- Parameters
-
model rigid body model Q N-element vector of generalized positions QDot N-element vector of generalized velocities QDDotDesired N-element vector of desired generalized accelerations ( 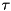 in the above equation)
in the above equation) CS Structure that contains information about the set of kinematic constraints. Note that the 'force' vector is appropriately updated after this function is called so that it contains the Lagrange multipliers. QDDotOutput N-element vector of generalized accelerations which satisfy the kinematic constraints ( 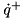 in the above equation)
in the above equation) TauOutput N-element vector of generalized forces which satisfy the the equations of motion for this constrained system. update_kinematics whether the kinematics of the model should be updated from Q.
f_ext External forces acting on the body in base coordinates (optional, defaults to NULL)
◆ InverseDynamicsConstraintsRelaxed()
| RBDL_DLLAPI void RigidBodyDynamics::InverseDynamicsConstraintsRelaxed | ( | Model & | model, |
| const Math::VectorNd & | Q, | ||
| const Math::VectorNd & | QDot, | ||
| const Math::VectorNd & | QDDotControls, | ||
| ConstraintSet & | CS, | ||
| Math::VectorNd & | QDDotOutput, | ||
| Math::VectorNd & | TauOutput, | ||
| bool | update_kinematics = true, |
||
| std::vector< Math::SpatialVector > * | f_ext = NULL |
||
| ) |
A relaxed inverse-dynamics operator that can be applied to under-actuated or fully-actuated constrained multibody systems.
- Important Set the actuated degrees-of-freedom using RigidBodyDynamics::ConstraintSet::SetActuationMap prior to calling this function.
- This function implements the relaxed inverse-dynamics operator defined by Koch [1] and Kudruss [2]. When given a vector of generalized positions, generalized velocities, and desired generalized accelerations will solve for a set of generalized accelerations and forces which satisfy the constrained equations of motion such that the solution is close to a vector of desired acceleration controls
s.t.![\[ \min{\ddot{q}} \dfrac{1}{2} \ddot{q}^T H \ddot{q} + C^T \ddot{q} + \dfrac{1}{2}(Sx-S\ddot{q})^{T} W (Sx-S\ddot{q}) \]](../../form_65.png)
In contrast to the RigidBodyDynamics::InverseDynamicsConstraints method, this method can work with underactuated systems. Mathematically this method does not depend on![\[ G \ddot{q} = \gamma. \]](../../form_66.png)
where![\[ \text{rank}(GP^T) < n-n_a \]](../../form_67.png)
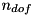 is the number of degrees of freedom and
is the number of degrees of freedom and 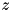 is the number of actuated degrees of freedom.
is the number of actuated degrees of freedom.
- For those readers who are unfamiliar with quadratic programs (QP), like the constrained minimization problem above, read the following important notes. One consequence of this additional flexibility is that the term
 should now be interpreted as a control vector:
should now be interpreted as a control vector:
- The minimum of the above constrained QP may not be
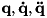 where
where 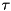 is the vector of desired accelerations. The terms
is the vector of desired accelerations. The terms 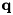 will
will 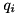 pull the solution away from this value and the constraint
pull the solution away from this value and the constraint 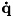 may make it impossible to exactly satisfy
may make it impossible to exactly satisfy 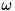 .
.
- Koch's original formulation has been modifed so that setting
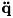 will yield a solution for
will yield a solution for 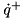 that is close to
that is close to 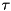 . However, even if an exact solution for
. However, even if an exact solution for 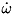 exists it will may not be realized using
exists it will may not be realized using 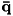 . Iteration may be required.
. Iteration may be required.
To solve the above constrained minimization problem we take the derivative of the above system of equations w.r.t. 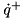 and
and 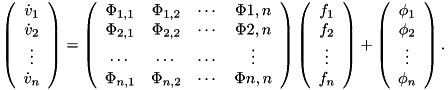 set the result to zero and solve. This results in the KKT system
set the result to zero and solve. This results in the KKT system
![\[ \left( \begin{array}{cc} H+K & G^T \\ G & 0 \end{array} \right) \left( \begin{array}{c} \ddot{q} \\ -\lambda \end{array} \right) =\left( \begin{array}{c} (S^T W S)x - C\\ \gamma \end{array} \right). \]](../../form_78.png)
This system of linear equations is not solved directly, but instead the null-space formulation presented in Sec. 2.5 of Koch as it is much faster. As with the RigidBodyDynamics::InverseDynamicsConstraints method the matrices 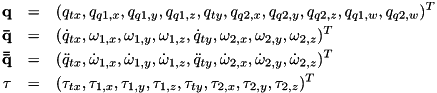 and
and 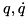 select the actuated and unactuated parts of
select the actuated and unactuated parts of
![\[\ddot{q} = S^T u + P^T v \]](../../form_81.png)
, and
![\[u^* = S^T x \]](../../form_82.png)
, where 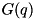 is a selection matrix that returns the actuated subspace of
is a selection matrix that returns the actuated subspace of  (
( 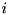 ) and
) and 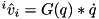 returns the unactuated subspace of
returns the unactuated subspace of 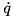 (
( 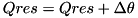 ).
).
![\[ \left( \begin{array}{ccc} S H S^T+W & S M P^T & S G^T \\ P M S^T & P M P^T & P G^T \\ G S^T & G P^T & 0 \end{array} \right) \left( \begin{array}{c} u \\ v \\ -\lambda \end{array} \right) = \left( \begin{array}{c} Wu^* -SC\\ -PC\\ \gamma \end{array} \right) \]](../../form_88.png)
This system has an upper block triangular structure which can be seen by noting that
![\[ J^T = \left( \begin{array}{c} S G^T \\ P G^T \end{array} \right), \]](../../form_89.png)
by grouping the upper 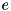 block into
block into
![\[ F = \left( \begin{array}{cc} SMS^T + W & SMP^T \\ PMS^T & PMP^T \end{array} \right), \]](../../form_91.png)
and by grouping the right hand side into
![\[ g = \left( \begin{array}{c} -Wu^* + SC \\ PC \end{array} \right) \]](../../form_92.png)
resulting in
![\[ \left( \begin{array}{cc} F & J^T \\ J & 0 \end{array} \right) \left( \begin{array}{c} p \\ -\lambda \end{array} \right) = \left( \begin{array}{c} -g \\ \gamma \end{array} \right) \]](../../form_93.png)
This system can be triangularized by projecting the system into the null space of 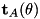 . First we begin with a QR decomposition of
. First we begin with a QR decomposition of 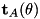 into
into
![\[ J^T = \left( Y \, Z \right)\left( \begin{array}{c} R \\ 0 \end{array} \right) \]](../../form_95.png)
and projecting 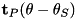 into the space
into the space ![$[Y,Z]$](../../form_97.png)
![\[ p = Y p_Y + Z p_Z. \]](../../form_98.png)
This allows us to express the previous KKT system as
![\[ \left( \begin{array}{ccc} Y^T F Y & Y^T F Z & R \\ Z^T F Y & Z^T F Z & 0 \\ R^T & 0 & 0 \end{array} \right) \left( \begin{array}{c} p_Y \\ p_Z \\ -\lambda \end{array} \right) = \left( \begin{array}{c} -Y^T g \\ -Z^T g \\ \gamma \end{array} \right) \]](../../form_99.png)
Though this system is still 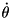 it can be solved in parts for
it can be solved in parts for 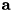
![\[ R^T p_Y = \gamma, \]](../../form_102.png)
and 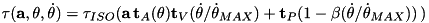
![\[ (Z^T F Z) p_Z = -(Z^T F Y)p_Y - Z^T g \]](../../form_104.png)
which is enough to yield a solution for
![\[\left( \begin{array}{c} u \\ v \end{array} \right) = (Y p_Y + Z p_Z) \]](../../form_105.png)
and finally
![\[ \ddot{q} = S^T u + P^T v. \]](../../form_106.png)
This method is less computationally expensive than the KKT system directly since
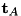 is of size
is of size 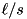 and
and 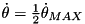 is of size
is of size 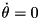 which is far smaller than the
which is far smaller than the 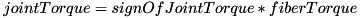 matrix used in the direct method. As it is relatively inexpensive, the dual variables are also evaluated
matrix used in the direct method. As it is relatively inexpensive, the dual variables are also evaluated
![\[ R \lambda = (Y^T FY)p_Y + (Y^T F Z)p_Z + Y^T g \]](../../form_112.png)
and
![\[ \tau = S^T W S (x-\ddot{q}) \]](../../form_113.png)
- Note
- Two modifications have been made to this implementation to bring the solution to
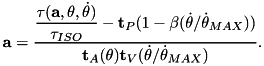 much closer to
much closer to 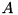
- The vector
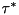 has been modifed to
has been modifed to 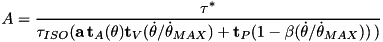 so that the term
so that the term 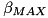 in the upper right hand side is compensated
in the upper right hand side is compensated - The weighting matrix
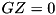 has a main diagional that is scaled to be uniformly 100 times larger than the biggest element in M. This will drive the solution closer to
has a main diagional that is scaled to be uniformly 100 times larger than the biggest element in M. This will drive the solution closer to  without hurting the scaling of the matrix too badly.
without hurting the scaling of the matrix too badly.
- The vector
- The Lagrange multipliers are solved for and stored in the ‘force’ field of the ConstraintSet structure.
-
The sign of
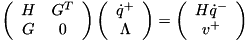 in this documentation is consistent with RBDL and it is equal to
in this documentation is consistent with RBDL and it is equal to 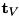 times the right hand side of the constraint expressed at the acceleration-level. It is more common to see
times the right hand side of the constraint expressed at the acceleration-level. It is more common to see 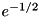 , in the literature and define
, in the literature and define 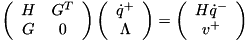 as the positive right-hand side of the acceleration equation.
as the positive right-hand side of the acceleration equation.
References
- Koch KH (2015). Using model-based optimal control for conceptional motion generation for the humannoid robot hrp-2 and design investigations for exo-skeletons. Heidelberg University (Doctoral dissertation).
- Kudruss M (under review as of May 2019). Nonlinear model-predictive control for the motion generation of humanoids. Heidelberg University (Doctoral dissertation)
- Parameters
-
model rigid body model Q N-element vector of generalized positions QDot N-element vector of generalized velocities QDDotControls N-element vector of generalized acceleration controls (  in the above equation). If the idea of a control vector is unclear please read the above text for additional details.
in the above equation). If the idea of a control vector is unclear please read the above text for additional details.CS Structure that contains information about the set of kinematic constraints. Note that the 'force' vector is appropriately updated after this function is called so that it contains the Lagrange multipliers. QDDotOutput N-element vector of generalized accelerations which satisfy the kinematic constraints ( 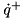 in the above equation)
in the above equation) TauOutput N-element vector of generalized forces which satisfy the the equations of motion for this constrained system.
update_kinematics whether the kinematics of the model should be updated from Q.
f_ext External forces acting on the body in base coordinates (optional, defaults to NULL)
◆ isBaumgarteStabilizationEnabled()
|
inline |
- Parameters
-
groupIndex the index number of this constraint (see getGroupIndex index functions)
- Returns
- true if Baumgarte stabilization is enabled
Definition at line 663 of file Constraints.h.
◆ isConstrainedSystemFullyActuated()
| RBDL_DLLAPI bool RigidBodyDynamics::isConstrainedSystemFullyActuated | ( | Model & | model, |
| const Math::VectorNd & | Q, | ||
| const Math::VectorNd & | QDot, | ||
| ConstraintSet & | CS, | ||
| bool | update_kinematics = true, |
||
| std::vector< Math::SpatialVector > * | f_ext = NULL |
||
| ) |
A method to evaluate if the constrained system is fully actuated.
- This method will evaluate the rank of
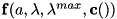 in order to assess if the constrained system is fully actuated or is under actuated. If the system is fully actuated the exact method RigidBodyDynamics::InverseDynamicsConstraints can be used, otherwise only relaxed method RigidBodyDynamics::InverseDynamicsConstraintsRelaxed can be used.
in order to assess if the constrained system is fully actuated or is under actuated. If the system is fully actuated the exact method RigidBodyDynamics::InverseDynamicsConstraints can be used, otherwise only relaxed method RigidBodyDynamics::InverseDynamicsConstraintsRelaxed can be used.
- Note
- This method uses a relatively slow but accurate method to evaluate the rank.
- Parameters
-
model rigid body model Q N-element vector of generalized positions QDot N-element vector of generalized velocities CS Structure that contains information about the set of kinematic constraints. update_kinematics whether the kinematics of the model should be updated from Q.
f_ext External forces acting on the body in base coordinates (optional, defaults to NULL)
◆ SetActuationMap()
| void SetActuationMap | ( | const Model & | model, |
| const std::vector< bool > & | actuatedDof | ||
| ) |
Initializes and allocates memory needed for InverseDynamicsConstraints and InverseDynamicsConstraintsRelaxed.
This function allocates the temporary vectors and matrices needed for the RigidBodyDynamics::InverseDynamicsConstraints and RigidBodyDynamics::InverseDynamicsConstraintsRelaxed methods. In addition, the constant matrices S and P are set here. This function needs to be called once before calling either RigidBodyDynamics::InverseDynamicsConstraints or RigidBodyDynamics::InverseDynamicsConstraintsRelaxed. It does not ever need be called again, unless the actuated degrees of freedom change, or the constraint set changes.
- Parameters
-
model rigid body model
actuatedDof : a vector that is q_size in length (or dof_count in length) which has a 'true' entry for every generalized degree-of freedom that is driven by an actuator and 'false' for every degree-of-freedom that is not.
◆ SetSolver()
|
inline |
Specifies which method should be used for solving undelying linear systems.
Definition at line 807 of file Constraints.h.
◆ size()
|
inline |
Returns the number of constraints.
Definition at line 849 of file Constraints.h.
◆ SolveConstrainedSystemDirect()
| RBDL_DLLAPI void RigidBodyDynamics::SolveConstrainedSystemDirect | ( | Math::MatrixNd & | H, |
| const Math::MatrixNd & | G, | ||
| const Math::VectorNd & | c, | ||
| const Math::VectorNd & | gamma, | ||
| Math::VectorNd & | lambda, | ||
| Math::MatrixNd & | A, | ||
| Math::VectorNd & | b, | ||
| Math::VectorNd & | x, | ||
| Math::LinearSolver & | linear_solver | ||
| ) |
Solves the full contact system directly, i.e. simultaneously for contact forces and joint accelerations.
This solves a  linear system.
linear system.
- Parameters
-
H the joint space inertia matrix G the constraint Jacobian c the  vector of the upper part of the right hand side of the system
vector of the upper part of the right hand side of the system gamma the 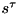 vector of the lower part of the right hand side of the system
vector of the lower part of the right hand side of the system lambda result: constraint forces A work-space for the matrix of the linear system b work-space for the right-hand-side of the linear system x work-space for the solution of the linear system linear_solver type of solver that should be used to solve the system
◆ SolveConstrainedSystemNullSpace()
| RBDL_DLLAPI void RigidBodyDynamics::SolveConstrainedSystemNullSpace | ( | Math::MatrixNd & | H, |
| const Math::MatrixNd & | G, | ||
| const Math::VectorNd & | c, | ||
| const Math::VectorNd & | gamma, | ||
| Math::VectorNd & | qddot, | ||
| Math::VectorNd & | lambda, | ||
| Math::MatrixNd & | Y, | ||
| Math::MatrixNd & | Z, | ||
| Math::VectorNd & | qddot_y, | ||
| Math::VectorNd & | qddot_z, | ||
| Math::LinearSolver & | linear_solver | ||
| ) |
Solves the contact system by first solving for the joint accelerations and then for the constraint forces.
This methods requires a 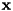 matrix of the form
matrix of the form ![$\left[ \ Y \ | Z \ \right]$](../../form_145.png) with the property
with the property  that can be computed using a QR decomposition (e.g. see code for ForwardDynamicsContactsNullSpace()).
that can be computed using a QR decomposition (e.g. see code for ForwardDynamicsContactsNullSpace()).
- Parameters
-
H the joint space inertia matrix G the constraint Jacobian c the 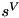 vector of the upper part of the right hand side of the system
vector of the upper part of the right hand side of the system gamma the 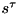 vector of the lower part of the right hand side of the system
vector of the lower part of the right hand side of the system qddot result: joint accelerations lambda result: constraint forces Y basis for the range-space of the constraints Z basis for the null-space of the constraints qddot_y work-space of size 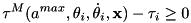
qddot_z work-space of size 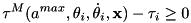
linear_solver type of solver that should be used to solve the system
◆ SolveConstrainedSystemRangeSpaceSparse()
| RBDL_DLLAPI void RigidBodyDynamics::SolveConstrainedSystemRangeSpaceSparse | ( | Model & | model, |
| Math::MatrixNd & | H, | ||
| const Math::MatrixNd & | G, | ||
| const Math::VectorNd & | c, | ||
| const Math::VectorNd & | gamma, | ||
| Math::VectorNd & | qddot, | ||
| Math::VectorNd & | lambda, | ||
| Math::MatrixNd & | K, | ||
| Math::VectorNd & | a, | ||
| Math::LinearSolver | linear_solver | ||
| ) |
Solves the contact system by first solving for the the joint accelerations and then the contact forces using a sparse matrix decomposition of the joint space inertia matrix.
This method exploits the branch-induced sparsity by the structure preserving 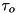 decomposition described in RBDL, Section 6.5.
decomposition described in RBDL, Section 6.5.
- Parameters
-
model rigid body model H the joint space inertia matrix G the constraint Jacobian c the 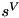 vector of the upper part of the right hand side of the system
vector of the upper part of the right hand side of the system gamma the 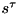 vector of the lower part of the right hand side of the system
vector of the lower part of the right hand side of the system qddot result: joint accelerations lambda result: constraint forces K work-space for the matrix of the constraint force linear system a work-space for the right-hand-side of the constraint force linear system linear_solver type of solver that should be used to solve the constraint force system
Variable Documentation
◆ A
Workspace for the Lagrangian left-hand-side matrix.
Definition at line 915 of file Constraints.h.
◆ a
Workspace for the accelerations of due to the test forces.
Definition at line 963 of file Constraints.h.
◆ b
Workspace for the Lagrangian right-hand-side.
Definition at line 917 of file Constraints.h.
◆ bound
| bool bound |
Whether the constraint set was bound to a model (mandatory!).
Definition at line 859 of file Constraints.h.
◆ C
Workspace for the coriolis forces.
Definition at line 908 of file Constraints.h.
◆ cache
| ConstraintCache cache |
Definition at line 990 of file Constraints.h.
◆ constraints
| std::vector< std::shared_ptr<Constraint> > constraints |
Definition at line 883 of file Constraints.h.
◆ constraintType
| std::vector<ConstraintType> constraintType |
Definition at line 862 of file Constraints.h.
◆ contactConstraints
| std::vector< std::shared_ptr<ContactConstraint> > contactConstraints |
Definition at line 885 of file Constraints.h.
◆ d_a
| std::vector<Math::SpatialVector> d_a |
Workspace for the acceleration due to the test force.
Definition at line 978 of file Constraints.h.
◆ d_d
| Math::VectorNd d_d |
Workspace when applying constraint forces.
Definition at line 986 of file Constraints.h.
◆ d_IA
| std::vector<Math::SpatialMatrix> d_IA |
Workspace for the inertia when applying constraint forces.
Definition at line 982 of file Constraints.h.
◆ d_multdof3_u
| std::vector<Math::Vector3d> d_multdof3_u |
Definition at line 988 of file Constraints.h.
◆ d_pA
| std::vector<Math::SpatialVector> d_pA |
Workspace for the bias force due to the test force.
Definition at line 976 of file Constraints.h.
◆ d_u
| Math::VectorNd d_u |
Definition at line 979 of file Constraints.h.
◆ d_U
| std::vector<Math::SpatialVector> d_U |
Workspace when applying constraint forces.
Definition at line 984 of file Constraints.h.
◆ err
| Math::VectorNd err |
Position error for the Baumgarte stabilization
Definition at line 891 of file Constraints.h.
◆ errd
| Math::VectorNd errd |
Velocity error for the Baumgarte stabilization
Definition at line 893 of file Constraints.h.
◆ F
Definition at line 935 of file Constraints.h.
◆ f_ext_constraints
| std::vector<Math::SpatialVector> f_ext_constraints |
Workspace for the actual spatial forces.
Definition at line 971 of file Constraints.h.
◆ f_t
| std::vector<Math::SpatialVector> f_t |
Workspace for the test forces.
Definition at line 969 of file Constraints.h.
◆ Fll
| Math::MatrixNd Fll |
Definition at line 936 of file Constraints.h.
◆ Flr
| Math::MatrixNd Flr |
Definition at line 936 of file Constraints.h.
◆ force
| Math::VectorNd force |
The Lagrange multipliers, which due to some careful normalization in the formulation of constraints are the constraint forces.
Definition at line 897 of file Constraints.h.
◆ Ful
| Math::MatrixNd Ful |
Definition at line 936 of file Constraints.h.
◆ Fur
| Math::MatrixNd Fur |
Definition at line 936 of file Constraints.h.
◆ G
Workspace for the constraint Jacobian.
Definition at line 912 of file Constraints.h.
◆ g
Definition at line 940 of file Constraints.h.
◆ gamma
| Math::VectorNd gamma |
Workspace of the right hand side of the acceleration equation.
Definition at line 910 of file Constraints.h.
◆ GPT
| Math::MatrixNd GPT |
Definition at line 952 of file Constraints.h.
◆ GPT_full_qr
| Eigen::FullPivHouseholderQR<Math::MatrixNd> GPT_full_qr |
Definition at line 948 of file Constraints.h.
◆ GT
Definition at line 938 of file Constraints.h.
◆ GT_qr
| Eigen::HouseholderQR<Math::MatrixNd> GT_qr |
Workspace for the QR decomposition of the null-space method.
Definition at line 947 of file Constraints.h.
◆ GT_qr_Q
| Math::MatrixNd GT_qr_Q |
Definition at line 951 of file Constraints.h.
◆ GTl
| Math::MatrixNd GTl |
Definition at line 939 of file Constraints.h.
◆ GTu
| Math::MatrixNd GTu |
Definition at line 939 of file Constraints.h.
◆ H
Workspace for the joint space inertia matrix.
Definition at line 906 of file Constraints.h.
◆ idGroupMap
| std::map< unsigned int, unsigned int> idGroupMap |
Definition at line 868 of file Constraints.h.
◆ impulse
| Math::VectorNd impulse |
Constraint impulses along the constraint directions.
Definition at line 899 of file Constraints.h.
◆ K
Workspace for the Inverse Articulated-Body Inertia.
Definition at line 961 of file Constraints.h.
◆ linear_solver
| Math::LinearSolver linear_solver |
Method that should be used to solve internal linear systems.
Definition at line 857 of file Constraints.h.
◆ loopConstraints
| std::vector< std::shared_ptr<LoopConstraint> > loopConstraints |
Definition at line 887 of file Constraints.h.
◆ name
| std::vector<std::string> name |
Definition at line 864 of file Constraints.h.
◆ nameGroupMap
| std::map< std::string, unsigned int > nameGroupMap |
Definition at line 866 of file Constraints.h.
◆ P
Selection matrix for the non-actuated parts of the model.
Definition at line 925 of file Constraints.h.
◆ point_accel_0
| std::vector<Math::Vector3d> point_accel_0 |
Workspace for the default point accelerations.
Definition at line 973 of file Constraints.h.
◆ py
Definition at line 942 of file Constraints.h.
◆ pz
Definition at line 943 of file Constraints.h.
◆ QDDot_0
| Math::VectorNd QDDot_0 |
Workspace for the default accelerations.
Definition at line 967 of file Constraints.h.
◆ QDDot_t
| Math::VectorNd QDDot_t |
Workspace for the test accelerations.
Definition at line 965 of file Constraints.h.
◆ qddot_y
| Math::VectorNd qddot_y |
Definition at line 956 of file Constraints.h.
◆ qddot_z
| Math::VectorNd qddot_z |
Definition at line 957 of file Constraints.h.
◆ R
Definition at line 955 of file Constraints.h.
◆ Ru
Definition at line 941 of file Constraints.h.
◆ S
Selection matrix for the actuated parts of the model needed for the inverse-dynamics-with-constraints operator
Definition at line 923 of file Constraints.h.
◆ u
Definition at line 932 of file Constraints.h.
◆ userDefinedIdGroupMap
| std::map< unsigned int, unsigned int> userDefinedIdGroupMap |
Definition at line 867 of file Constraints.h.
◆ v
Definition at line 933 of file Constraints.h.
◆ v_plus
| Math::VectorNd v_plus |
The velocities we want to have along the constraint directions.
Definition at line 901 of file Constraints.h.
◆ W
Matrix that holds the relative cost of deviating from the desired accelerations
Definition at line 928 of file Constraints.h.
◆ Winv
| Math::MatrixNd Winv |
Definition at line 929 of file Constraints.h.
◆ WinvSC
| Math::VectorNd WinvSC |
Definition at line 930 of file Constraints.h.
◆ x
Workspace for the Lagrangian solution.
Definition at line 919 of file Constraints.h.
◆ Y
Definition at line 953 of file Constraints.h.
◆ Z
Definition at line 954 of file Constraints.h.