Namespaces | |
| namespace | Addons |
| namespace | Errors |
| namespace | Math |
| Math types such as vectors and matrices and utility functions. | |
| namespace | Utils |
| Namespace that contains optional helper functions. | |
Data Structures | |
| struct | Body |
| Describes all properties of a single body. More... | |
| class | Constraint |
| Interface to define general-purpose constraints. More... | |
| struct | ConstraintCache |
| struct | ConstraintSet |
| Structure that contains both constraint information and workspace memory. More... | |
| class | ContactConstraint |
| Implements a rigid kinematic body-point–to–ground constraint along a normal direction as described in Ch. 11 of Featherstone's Rigid Body Dynamics Algorithms book. More... | |
| struct | FixedBody |
| Keeps the information of a body and how it is attached to another body. More... | |
| struct | InverseKinematicsConstraintSet |
| class | LoopConstraint |
| Implements a rigid kinematic loop (or body-to-body) constraints as described in Ch. 8 of Featherstone's Rigid Body Dynamics Algorithms book. More... | |
Enumerations | |
| enum | ConstraintType { ConstraintTypeContact =0 , ConstraintTypeLoop , ConstraintTypeCustom , ConstraintTypeLast } |
| Enum to describe the type of a constraint. More... | |
Functions | |
| RBDL_DLLAPI void | jcalc (Model &model, unsigned int joint_id, const VectorNd &q, const VectorNd &qdot) |
| RBDL_DLLAPI Math::SpatialTransform | jcalc_XJ (Model &model, unsigned int joint_id, const Math::VectorNd &q) |
| RBDL_DLLAPI void | jcalc_X_lambda_S (Model &model, unsigned int joint_id, const VectorNd &q) |
| RBDL_DLLAPI void | UpdateKinematics (Model &model, const Math::VectorNd &Q, const Math::VectorNd &QDot, const Math::VectorNd &QDDot) |
| Updates and computes velocities and accelerations of the bodies. More... | |
| RBDL_DLLAPI void | UpdateKinematicsCustom (Model &model, const Math::VectorNd *Q, const Math::VectorNd *QDot, const Math::VectorNd *QDDot) |
| Selectively updates model internal states of body positions, velocities and/or accelerations. More... | |
| RBDL_DLLAPI Vector3d | CalcBodyToBaseCoordinates (Model &model, const Math::VectorNd &Q, unsigned int body_id, const Math::Vector3d &body_point_position, bool update_kinematics=true) |
| Returns the base coordinates of a point given in body coordinates. More... | |
| RBDL_DLLAPI Vector3d | CalcBaseToBodyCoordinates (Model &model, const Math::VectorNd &Q, unsigned int body_id, const Math::Vector3d &base_point_position, bool update_kinematics=true) |
| Returns the body coordinates of a point given in base coordinates. More... | |
| RBDL_DLLAPI Matrix3d | CalcBodyWorldOrientation (Model &model, const Math::VectorNd &Q, const unsigned int body_id, bool update_kinematics=true) |
| Returns the orientation of a given body as 3x3 matrix. More... | |
| RBDL_DLLAPI void | CalcPointJacobian (Model &model, const Math::VectorNd &Q, unsigned int body_id, const Math::Vector3d &point_position, Math::MatrixNd &G, bool update_kinematics=true) |
| Computes the point jacobian for a point on a body. More... | |
| RBDL_DLLAPI void | CalcPointJacobian6D (Model &model, const Math::VectorNd &Q, unsigned int body_id, const Math::Vector3d &point_position, Math::MatrixNd &G, bool update_kinematics=true) |
| Computes a 6-D Jacobian for a point on a body. More... | |
| RBDL_DLLAPI void | CalcBodySpatialJacobian (Model &model, const Math::VectorNd &Q, unsigned int body_id, Math::MatrixNd &G, bool update_kinematics=true) |
| Computes the spatial jacobian for a body. More... | |
| RBDL_DLLAPI Vector3d | CalcPointVelocity (Model &model, const Math::VectorNd &Q, const Math::VectorNd &QDot, unsigned int body_id, const Math::Vector3d &point_position, bool update_kinematics=true) |
| Computes the velocity of a point on a body. More... | |
| RBDL_DLLAPI Math::SpatialVector | CalcPointVelocity6D (Model &model, const Math::VectorNd &Q, const Math::VectorNd &QDot, unsigned int body_id, const Math::Vector3d &point_position, bool update_kinematics=true) |
| Computes angular and linear velocity of a point that is fixed on a body. More... | |
| RBDL_DLLAPI Vector3d | CalcPointAcceleration (Model &model, const Math::VectorNd &Q, const Math::VectorNd &QDot, const Math::VectorNd &QDDot, unsigned int body_id, const Math::Vector3d &point_position, bool update_kinematics=true) |
| Computes the linear acceleration of a point on a body. More... | |
| RBDL_DLLAPI SpatialVector | CalcPointAcceleration6D (Model &model, const Math::VectorNd &Q, const Math::VectorNd &QDot, const Math::VectorNd &QDDot, unsigned int body_id, const Math::Vector3d &point_position, bool update_kinematics=true) |
| Computes linear and angular acceleration of a point on a body. More... | |
| RBDL_DLLAPI bool | InverseKinematics (Model &model, const Math::VectorNd &Qinit, const std::vector< unsigned int > &body_id, const std::vector< Math::Vector3d > &body_point, const std::vector< Math::Vector3d > &target_pos, Math::VectorNd &Qres, double step_tol=1.0e-12, double lambda=0.01, unsigned int max_iter=55) |
| Computes the inverse kinematics iteratively using a damped Levenberg-Marquardt method (also known as Damped Least Squares method) More... | |
| RBDL_DLLAPI Vector3d | CalcAngularVelocityfromMatrix (const Matrix3d &RotMat) |
| RBDL_DLLAPI bool | InverseKinematics (Model &model, const Math::VectorNd &Qinit, InverseKinematicsConstraintSet &CS, Math::VectorNd &Qres) |
| RBDL_DLLAPI void | CalcConstraintsPositionError (Model &model, const Math::VectorNd &Q, ConstraintSet &CS, Math::VectorNd &errOutput, bool update_kinematics=true) |
| Computes the position errors for the given ConstraintSet. More... | |
| RBDL_DLLAPI void | CalcConstraintsJacobian (Model &model, const Math::VectorNd &Q, ConstraintSet &CS, Math::MatrixNd &GOutput, bool update_kinematics=true) |
| Computes the Jacobian for the given ConstraintSet. More... | |
| RBDL_DLLAPI void | CalcConstraintsVelocityError (Model &model, const Math::VectorNd &Q, const Math::VectorNd &QDot, ConstraintSet &CS, Math::VectorNd &errOutput, bool update_kinematics=true) |
| Computes the velocity errors for the given ConstraintSet. More... | |
| RBDL_DLLAPI void | CalcConstrainedSystemVariables (Model &model, const Math::VectorNd &Q, const Math::VectorNd &QDot, const Math::VectorNd &Tau, ConstraintSet &CSOutput, bool update_kinematics=true, std::vector< Math::SpatialVector > *f_ext=NULL) |
Computes the terms 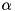 , , 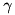 , and , and 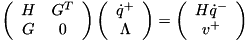 of the constrained dynamic problem and stores them in the ConstraintSet. More... of the constrained dynamic problem and stores them in the ConstraintSet. More... | |
| RBDL_DLLAPI bool | CalcAssemblyQ (Model &model, Math::VectorNd QInit, ConstraintSet &CS, Math::VectorNd &QOutput, const Math::VectorNd &weights, double tolerance=1e-12, unsigned int max_iter=100) |
| Computes a feasible initial value of the generalized joint positions. More... | |
| RBDL_DLLAPI void | CalcAssemblyQDot (Model &model, const Math::VectorNd &Q, const Math::VectorNd &QDotInit, ConstraintSet &CS, Math::VectorNd &QDotOutput, const Math::VectorNd &weights) |
| Computes a feasible initial value of the generalized joint velocities. More... | |
| RBDL_DLLAPI void | ForwardDynamicsConstraintsDirect (Model &model, const Math::VectorNd &Q, const Math::VectorNd &QDot, const Math::VectorNd &Tau, ConstraintSet &CS, Math::VectorNd &QDDotOutput, bool update_kinematics=true, std::vector< Math::SpatialVector > *f_ext=NULL) |
| Computes forward dynamics with contact by constructing and solving the full lagrangian equation. More... | |
| RBDL_DLLAPI void | ForwardDynamicsConstraintsRangeSpaceSparse (Model &model, const Math::VectorNd &Q, const Math::VectorNd &QDot, const Math::VectorNd &Tau, ConstraintSet &CS, Math::VectorNd &QDDotOutput, bool update_kinematics=true, std::vector< Math::SpatialVector > *f_ext=NULL) |
| RBDL_DLLAPI void | ForwardDynamicsConstraintsNullSpace (Model &model, const Math::VectorNd &Q, const Math::VectorNd &QDot, const Math::VectorNd &Tau, ConstraintSet &CS, Math::VectorNd &QDDotOutput, bool update_kinematics=true, std::vector< Math::SpatialVector > *f_ext=NULL) |
| RBDL_DLLAPI void | ForwardDynamicsContactsKokkevis (Model &model, const Math::VectorNd &Q, const Math::VectorNd &QDot, const Math::VectorNd &Tau, ConstraintSet &CS, Math::VectorNd &QDDotOutput) |
| Computes forward dynamics that accounts for active contacts in ConstraintSet. More... | |
| RBDL_DLLAPI void | InverseDynamicsConstraintsRelaxed (Model &model, const Math::VectorNd &Q, const Math::VectorNd &QDot, const Math::VectorNd &QDDotControls, ConstraintSet &CS, Math::VectorNd &QDDotOutput, Math::VectorNd &TauOutput, bool update_kinematics=true, std::vector< Math::SpatialVector > *f_ext=NULL) |
| A relaxed inverse-dynamics operator that can be applied to under-actuated or fully-actuated constrained multibody systems. More... | |
| RBDL_DLLAPI void | InverseDynamicsConstraints (Model &model, const Math::VectorNd &Q, const Math::VectorNd &QDot, const Math::VectorNd &QDDotDesired, ConstraintSet &CS, Math::VectorNd &QDDotOutput, Math::VectorNd &TauOutput, bool update_kinematics=true, std::vector< Math::SpatialVector > *f_ext=NULL) |
| An inverse-dynamics operator that can be applied to fully-actuated constrained systems. More... | |
| RBDL_DLLAPI bool | isConstrainedSystemFullyActuated (Model &model, const Math::VectorNd &Q, const Math::VectorNd &QDot, ConstraintSet &CS, bool update_kinematics=true, std::vector< Math::SpatialVector > *f_ext=NULL) |
| A method to evaluate if the constrained system is fully actuated. More... | |
| RBDL_DLLAPI void | ComputeConstraintImpulsesDirect (Model &model, const Math::VectorNd &Q, const Math::VectorNd &QDotMinus, ConstraintSet &CS, Math::VectorNd &QDotPlusOutput) |
| Computes contact gain by constructing and solving the full lagrangian equation. More... | |
| RBDL_DLLAPI void | ComputeConstraintImpulsesRangeSpaceSparse (Model &model, const Math::VectorNd &Q, const Math::VectorNd &QDotMinus, ConstraintSet &CS, Math::VectorNd &QDotPlusOutput) |
| Resolves contact gain using SolveContactSystemRangeSpaceSparse() More... | |
| RBDL_DLLAPI void | ComputeConstraintImpulsesNullSpace (Model &model, const Math::VectorNd &Q, const Math::VectorNd &QDotMinus, ConstraintSet &CS, Math::VectorNd &QDotPlusOutput) |
| Resolves contact gain using SolveContactSystemNullSpace() More... | |
| RBDL_DLLAPI void | SolveConstrainedSystemDirect (Math::MatrixNd &H, const Math::MatrixNd &G, const Math::VectorNd &c, const Math::VectorNd &gamma, Math::VectorNd &lambda, Math::MatrixNd &A, Math::VectorNd &b, Math::VectorNd &x, Math::LinearSolver &linear_solver) |
| Solves the full contact system directly, i.e. simultaneously for contact forces and joint accelerations. More... | |
| RBDL_DLLAPI void | SolveConstrainedSystemRangeSpaceSparse (Model &model, Math::MatrixNd &H, const Math::MatrixNd &G, const Math::VectorNd &c, const Math::VectorNd &gamma, Math::VectorNd &qddot, Math::VectorNd &lambda, Math::MatrixNd &K, Math::VectorNd &a, Math::LinearSolver linear_solver) |
| Solves the contact system by first solving for the the joint accelerations and then the contact forces using a sparse matrix decomposition of the joint space inertia matrix. More... | |
| RBDL_DLLAPI void | SolveConstrainedSystemNullSpace (Math::MatrixNd &H, const Math::MatrixNd &G, const Math::VectorNd &c, const Math::VectorNd &gamma, Math::VectorNd &qddot, Math::VectorNd &lambda, Math::MatrixNd &Y, Math::MatrixNd &Z, Math::VectorNd &qddot_y, Math::VectorNd &qddot_z, Math::LinearSolver &linear_solver) |
| Solves the contact system by first solving for the joint accelerations and then for the constraint forces. More... | |
| RBDL_DLLAPI void | InverseDynamics (Model &model, const Math::VectorNd &Q, const Math::VectorNd &QDot, const Math::VectorNd &QDDot, Math::VectorNd &Tau, std::vector< Math::SpatialVector > *f_ext=NULL) |
| Computes inverse dynamics with the Newton-Euler Algorithm. More... | |
| RBDL_DLLAPI void | NonlinearEffects (Model &model, const Math::VectorNd &Q, const Math::VectorNd &QDot, Math::VectorNd &Tau, std::vector< Math::SpatialVector > *f_ext=NULL) |
| Computes the coriolis forces. More... | |
| RBDL_DLLAPI void | CompositeRigidBodyAlgorithm (Model &model, const Math::VectorNd &Q, Math::MatrixNd &H, bool update_kinematics=true) |
| Computes the joint space inertia matrix by using the Composite Rigid Body Algorithm. More... | |
| RBDL_DLLAPI void | ForwardDynamics (Model &model, const Math::VectorNd &Q, const Math::VectorNd &QDot, const Math::VectorNd &Tau, Math::VectorNd &QDDot, std::vector< Math::SpatialVector > *f_ext=NULL) |
| Computes forward dynamics with the Articulated Body Algorithm. More... | |
| RBDL_DLLAPI void | ForwardDynamicsLagrangian (Model &model, const Math::VectorNd &Q, const Math::VectorNd &QDot, const Math::VectorNd &Tau, Math::VectorNd &QDDot, Math::LinearSolver linear_solver=Math::LinearSolverColPivHouseholderQR, std::vector< Math::SpatialVector > *f_ext=NULL, Math::MatrixNd *H=NULL, Math::VectorNd *C=NULL) |
| Computes forward dynamics by building and solving the full Lagrangian equation. More... | |
| RBDL_DLLAPI void | CalcMInvTimesTau (Model &model, const Math::VectorNd &Q, const Math::VectorNd &Tau, Math::VectorNd &QDDot, bool update_kinematics=true) |
| Computes the effect of multiplying the inverse of the joint space inertia matrix with a vector in linear time. More... | |
Detailed Description
This abstract class represents a mathematical function that calculates a value of arbitrary type based on M real arguments. The output type is set as a template argument, while the number of input components may be determined at runtime. The name "Function" (with no trailing _) may be used as a synonym for Function_<double>.
Subclasses define particular mathematical functions. Predefined subclasses are provided for several common function types: Function_<T>::Constant, Function_<T>::Linear, Function_<T>::Polynomial, and Function_<T>::Step. You can define your own subclasses for other function types. The Spline_ class also provides a convenient way to create various types of Functions.
This is a low level Quintic Bezier curve class that contains functions to design continuous sets of 'C' shaped Bezier curves, and to evaluate their values and derivatives. A set in this context is used to refer to 2 or more quintic Bezier curves that are continuously connected to eachother to form one smooth curve, hence the name QuinticBezierSet.
In the special case when this class is being used to generate and evaluate 2D Bezier curves, that is x(u) and y(u), there are also functions to evaluate y(x), the first six derivatives of y(x), and also the first integral of y(x).
This class was not designed to be a stand alone Quintic Bezier class, but rather was developed out of necessity to model muscles. I required curves that, when linearly extrapolated, were C2 continuous, and by necessity I had to use quintic Bezier curves. In addition, the curves I was developing were functions in x,y space, allowing many of the methods (such as the evaluation of y(x) given that x(u) and y(u), the derivatives of y(x), and its first integral) to be developed, though in general this can't always be done.
I have parcelled all of these tools into their own class so that others may more easily use and develop this starting point for their own means. I used the following text during the development of this code:
Mortenson, Michael E (2006). Geometric Modeling Third Edition. Industrial Press Inc., New York. Chapter 4 was quite helpful.
Future Upgrades
Analytical Inverse to x(u): I think this is impossible because it is not possible, in general, to find the roots to a quintic polynomial, however, this fact may not preclude forming the inverse curve. The impossibility of finding the roots to a quintic polynomial was proven by Abel (Abel's Impossibility Theorem) and Galois
http://mathworld.wolfram.com/QuinticEquation.html
At the moment I am approximating the curve u(x) using cubic splines to return an approximate value for u(x), which I polish using Newton's method to the desired precision.
Note as of Nov 2015** -> The cubic spline approximation of the inverse curve has been removed. Since there is no spline class in RBDL (and I'm not motivated to port it over from SimTK) this functionality does not work. In addition, I've since found that this nice inverse only saves a few Newton iterations over a calculated guess. It's not worth the effort to include.
Analytical Integral of y(x): This is possible using the Divergence Theorem applied to 2D curves. A nice example application is shown in link 2 for computing the area of a closed cubic Bezier curve. While I have been able to get the simple examples to work, I have failed to successfully compute the area under a quintic Bezier curve correctly. I ran out of time trying to fix this problem, and so at the present time I am numerically computing the integral at a number of knot points and then evaluating the spline to compute the integral value.
a. http://en.wikipedia.org/wiki/Divergence_theorem b. http://objectmix.com/graphics/133553-area-closed-bezier-curve.html
Note as of Nov 2015** -> The splined numeric integral of the curve has been removed. There is not an error-controlled numerical integrator in RBDL and so it is not straight forward to include this feature. -> For later: discuss options with Martin.
- calcU: Currently the Bezier curve value and its derivative are computed separately to evaluate f and df in the Newton iteration to solve for u(x). Code optimized to compute both of these quantites at the same time could cut the cost of evaluating x(u) and dx/du in half. Since these quantities are evaluated in an iterative loop, this one change could yield substantial computational savings.
- calcIndex: The function calcIndex computes which spline the contains the point of interest. This function has been implemented assuming a small number of Bezier curve sets, and so it simply linearly scans through the sets to determine the correct one to use. This function should be upgraded to use the bisection method if large quintic Bezier curve sets are desired.
- The addition of additional Bezier control point design algorithms, to create 'S' shaped curves, and possibly do subdivision.
- Low level Code Optimization: I have exported all of the low level code as optimized code from Maple. Although the code produced using this means is reasonably fast, it is usally possible to obtain superior performance (and sometimes less round off error) by doing this work by hand.
Computational Cost Details All computational costs assume the following operation costs:
Operation Type : #flops
+,-,=,Boolean Op : 1
/ : 10
sqrt: 20
trig: 40
These relative weightings will vary processor to processor, and so any of the quoted computational costs are approximate.
RBDL Port Notes
The port of this code from OpenSim has been accompanied by a few changes:
- The 'calcIntegral' method has been removed. Why? This function relied on having access to a variable-step error controlled integrator. There is no such integrator built into RBDL. Rather than add a dependency (by using Boost perhaps) this functionality has been removed.
- The function name .printMuscleCurveToFile(...) has been changed to .printCurveToFile().
- There have been some improvements to the function calcU in the SegmentedQuinticBezierToolkit.cc code. This function evaluates u such that x(u) - x* = 0. This is done using a Newton method. However, because these curves can be very nonlinear, the Newton method requires a very good initial start. In the OpenSim version this good initial guess was provided by splined interpolation of u(x). In the RBDL version this initial guess is provided by using a bisection method until the error of x(u)-x* is within sqrt(sqrt(tol)) or 2 Newton steps of the desired tolerance.
- Version
- 0.0
This class contains the quintic Bezier curves, x(u) and y(u), that have been created by SmoothSegmentedFunctionFactory to follow a physiologically meaningful muscle characteristic. A SmoothSegmentedFunction cannot be created directly,you must use SmoothSegmentedFunctionFactory to create the muscle curve of interest.
Computational Cost Details All computational costs assume the following operation costs:
Operation Type : #flops
+,-,=,Boolean Op : 1
/ : 10
sqrt: 20
trig: 40These relative weightings will vary processor to processor, and so any of the quoted computational costs are approximate.
RBDL Port Notes The port of this code from OpenSim has been accompanied by a few changes:
- The 'calcIntegral' method has been removed. Why? This function relied on having access to a variable-step error controlled integrator. There is no such integrator built into RBDL. Rather than add a dependency (by using Boost perhaps) this functionality has been removed.
The function name .printMuscleCurveToFile(...) has been changed to .printCurveToFile().
- Version
- 0.0
This is a class that acts as a user friendly wrapper to QuinticBezerCurveSet to build specific kinds of physiologically plausible muscle curves using C2 continuous sets of quintic Bezier curves. This class has been written there did not exist a set of curves describing muscle characteristics that was:
- Physiologically Accurate
- Continuous to the second derivative
- Parameterized in a physically meaningful manner
For example, the curves employed by Thelen (Thelen DG(2003). Adjustment of Muscle Mechanics Model Parameters to Simulate Dynamic Contractions in Older Adults. ASME Journal of Biomechanical Engineering (125).) are parameterized in a physically meaningful manner, making them easy to use. However there are many shortcomings of these curves:
- The tendon and parallel element are not C2 continuous, making them slow to simulate and likely not physiologically accurate.
- The active force length curve approaches does not achieve its minimum value at a normalized fiber length of 0.5, and 1.5.
- The force velocity curve is not C2 continuous at the origin. As it is written in the paper the curve is impossible to use with an equilibrium model because it is not invertible. In addition the force-velocity curve actually increases in stiffness as activation drops - a very undesirable property given that many muscles are inactive at any one time.
The muscle curves used in the literature until 2012 have been hugely influenced by Thelen's work, and thus similar comments can easily be applied to just about every other musculoskeletal simulation.
Another example is from Miller (Miller,RH(2011).Optimal Control of Human Running. PhD Thesis). On pg 149 a physiolgically plausible force velocity curve is specified that gives the user the ability to change the concentric curvature to be consistent with a slow or a fast twitch musle. This curve is not C2 continuous at the origin, but even worse, it contains singularities in its parameter space. Since these parameters do not have a physical interpretation this model is difficult to use without accidentically creating a curve with a singularity.
With this motivation I set out to develop a class that could generate muscle characteristic curves with the following properties:
- Physiologically Accurate
- Continuous to the second derivative
- Parameterized in a physically meaningful manner
- Monotonicity for monotonic curves
- Computationally efficient
These goals were surprisingly time consuming achieve, but these goals have been achieved using sets of C2 continuous quintic Bezier curves. The resulting muscle curve functions in this class take parameters that would be intuitive to biomechanists who simulate human musculoskeletal systems, and returns a SmoothSegmentedFunction which is capable of evaluating the value, and derivatives of the desired function (or actually relation as the case may be).
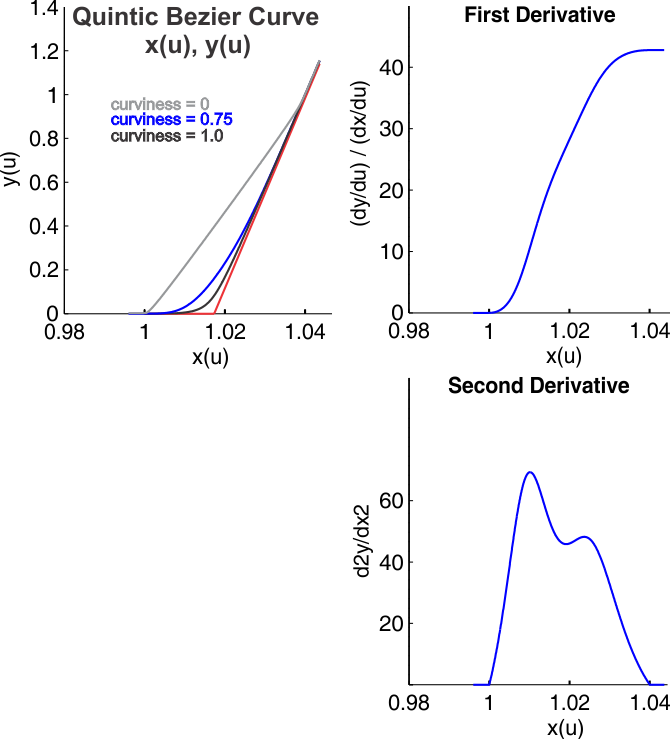
Each curve is made up of one or more C2 quintic Bezier curves x(u), and y(u), with linearily extrapolated ends as shown in the figure below. These quintic curves span 2 points, and achieve the desired derivative at its end points. The degree of curviness can be varied from 0 to 1 (0, 0.75 and 1.0 are shown in the figure in grey, blue and black respectively), and will make the curve approximate a line when set to 0 (grey), and approximate a curve that hugs the intersection of the lines that are defined by the end points locations and the slopes at the end of each curve segment (red lines). Although you do not need to set all of this information directly, for some of the curves it is useful to know that both the slope and the curviness parameter may need to be altered to achieve the desired shape.
Computational Cost Details All computational costs assume the following operation costs:
Operation Type : #flops *,+,-,=,Boolean Op : 1 / : 10 sqrt: 20 trig: 40
These relative weightings will vary processor to processor, and so any of the quoted computational costs are approximate.
RBDL Port Notes The port of this code from OpenSim has been accompanied by a few changes:
- The 'calcIntegral' method has been removed. Why? This function relied on having access to a variable-step error controlled integrator. There is no such integrator built into RBDL. Rather than add a dependency (by using Boost perhaps) this functionality has been removed.
- The function name .printMuscleCurveToFile(...) has been changed to .printCurveToFile().
- Version
- 0.0
Enumeration Type Documentation
◆ ConstraintType
| enum ConstraintType |
Enum to describe the type of a constraint.
| Enumerator | |
|---|---|
| ConstraintTypeContact | |
| ConstraintTypeLoop | |
| ConstraintTypeCustom | |
| ConstraintTypeLast | |
Definition at line 18 of file Constraint.h.
Function Documentation
◆ jcalc()
| RBDL_DLLAPI void RigidBodyDynamics::jcalc | ( | Model & | model, |
| unsigned int | joint_id, | ||
| const VectorNd & | q, | ||
| const VectorNd & | qdot | ||
| ) |
Definition at line 49 of file Joint.cc.
References std::cos(), SpatialTransform::E, jcalc_X_lambda_S(), jcalc_XJ(), std::sin(), and sincosp().
◆ jcalc_X_lambda_S()
| RBDL_DLLAPI void RigidBodyDynamics::jcalc_X_lambda_S | ( | Model & | model, |
| unsigned int | joint_id, | ||
| const VectorNd & | q | ||
| ) |
Definition at line 403 of file Joint.cc.
References std::cos(), SpatialTransform::E, jcalc_XJ(), std::sin(), and sincosp().
◆ jcalc_XJ()
| RBDL_DLLAPI Math::SpatialTransform RigidBodyDynamics::jcalc_XJ | ( | Model & | model, |
| unsigned int | joint_id, | ||
| const Math::VectorNd & | q | ||
| ) |
Definition at line 350 of file Joint.cc.
References RigidBodyDynamics::Math::Xrot(), and RigidBodyDynamics::Math::Xtrans().